Аннотация. В работе предложено соединить концепт покоящегося, кругового, осциллирующего, оставляющего бытие в глобальном смысле без изменений, времени Парменида, и концепт линейного, обладающего прошлым, настоящим и будущим, времени Гераклита, в их суперпозицию, которую в первом приближении можно образно представить в виде спирали. Но если спираль есть простая сумма двух движений – вращательного и поступательного, то суперпозиция предполагает более сложную их комбинацию, зависящую от фазы осциллирующего времени. Подобное рассмотрение позволяет прояснить такие понятия и парадоксы, как эмерджентность, являющаяся экспликацией нового качества, длительность Бергсона, концепт времени как негации вечности у Гегеля и, наконец, один из самых экзотических парадоксов современности – предложенную Эвереттом многомировую интерпретацию квантовой механики.
Ключевые слова: время, диалектика, квантовая механика, координата, скорость, эволюция, Эверетт, время возвращения Пуанкаре, фазовое пространство.
Предисловие
Начиная практически любую статью, и написав несколько предложений, вдруг обнаруживаешь, что для их прояснения необходимо предварить их ещё несколькими предложениями, а эти – другими и так до тех пор, пока мысль не замкнётся. Так проявляется диалектика мысли и также эксплицируется её темпоральность. С одной стороны, мы пришли к тому, с чего начинали, с другой стороны, то, к чему мы пришли, всё же несколько отличается от начала. Так появляется гегелевское снятие: «оттого, что нечто снимает себя, оно не превращается в ничто» [6, с. 110], и которое подобно стружке, снимаемой стамеской, и которое может не обрываться на многих оборотах заготовки, стоящей в токарном станке (При этом заготовка не меняется в собственном объёме). Понятие снятия в современной интерпретации звучит как эмерджентность. Чтобы такое было возможно, в становлении сущности должно участвовать ничто, на что обращали внимание и Гегель, и Платон. «Итак, раз существующее участвует в небытии и несуществующее — в бытии, то и единому, поскольку оно не существует, необходимо участвовать в бытии, чтобы не существовать» [13, с. 80]. Удивительно, как «снятие стружки» с самого термина снятие привело к появлению более длинного слова –эмерджентность. И не сложно заметить, что стамеской в данном образе выступает само время. Если её режущий край затупился, то заготовка неизменно проскальзывает, оставаясь неизменной в своём вращении, и наоборот, если резец сильнее войдёт в заготовку, превысив некоторый максимум, то заготовка разорвётся. Так происходят катастрофы.
Древние уже знали всё
О понятии времени человек должен был начать задумываться, как только он научился рефлексировать, поскольку рефлексия – это обнаружение корреляций и повторов или, как бы выразились математики, симметрий. Мир – это не просто некий поток перцепций, но он упорядочен некоторым образом. А самая главная корреляция – это связь вещей во времени, их последовательность.
Возможность течения времени с разной скоростью, меняющейся от нуля, то, что называется неизменностью и постоянством, до больших значений, когда всё рушится, заметили ещё в древности. Подобный феномен можно назвать центральным парадоксом времени.Антиномия постоянства и изменчивости прекрасно продемонстрирована в диалоге «Парменид» на примере понятия единого. «Следовательно, единое не движется ни одним видом движения»[13, с. 34] и «выходит, таким образом, что оно (единое) становится и моложе и старше себя» [13, с. 61]. Парадоксальность подобного описания заключается в том, что, с одной стороны, единое постоянно меняется внутри себя, что собственно было подмечено Гераклитом в его ставшей классической фразе: «в одну реку нельзя войти дважды». С другой стороны, несмотря на изменчивость, единое остаётся неизменным, причём не только в трёхмерном пространстве, но, как это видно из цитат, и во времени тоже. Если воспользоваться терминологией современной физики, то единое остаётся неизменным в четырёхмерном пространстве-времени. Такое пространство можно представить, как трёхмерные слои, образующиеся в каждое новое мгновение вдоль оси времени и соблюдающие чёткую очерёдность. В подобном представлении невозможно, чтобы причина произошла раньше следствия, что обосновывается постулатом Эйнштейна о невозможности превысить скорость света, ив рамках концепции Минковского бытие возможно только внутри так называемого светового конуса, ограничивающего возможные скорости скоростью света.
В современной интерпретации единое античных философов соответствует фазовому пространству возможных состояний некоторой сущности, иными словами, системы. Фазовое пространство, появившееся вместе с механикой Лагранжа и Гамильтона, описывает все возможные трансформации сущности и представляет собой -мерное пространство, где n – количество координат, необходимых для определения местоположения сущности. Но в определении этой механики для описания сущности недостаточно набора координат её месторасположения, ещё необходим набор скоростей. Существенно для нашего представления, что в подобном описании произвольная сущность возвращается к своему первоначальному состоянию. Если быть точнее, то она возвращается в некоторую окрестность своей стартовой точки.Теория, описывающая такое возвращение, связана с теорией хаоса и теорией динамических систем, активно развивающихся в настоящее время, и называется временем возвращения Пуанкаре. Доказательство подобного утверждения достаточно просто: поскольку фазовое пространство ограничено, а сущность имеет некоторый объём, то перемещаясь внутри собственных трансформаций, она должна вернуться к истоку. «Несколько парадоксальным выводом из теорем Пуанкаре и Лиувилля является следующее: если открыть перегородку, разделяющую камеру с газом и камеру с вакуумом, то через некоторое время молекулы газа почти наверное снова соберутся в первой камере. Разгадка парадокса в том, что некоторое время больше времени существования Солнечной системы»[2, с.67]. Удивительно то, что, с одной стороны сущность должна вернуться к почти начальному состоянию, но с другой стороны, согласно этой же теореме, это возвращение будет не совсем в точности воспроизводить начальное, как это показано на рис.1.
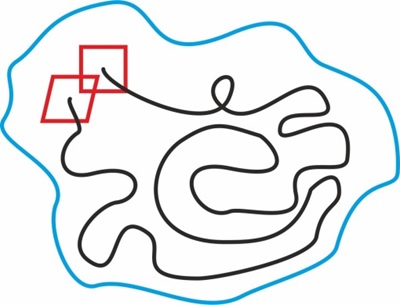
Рис. 1
И в связи с этим неполным подобием появляется понятие об эмерджентности и невозможности эталонов, на которых зиждется вся современная физика. «Но можно выбрать один предмет, ЭТАЛОН, и назвать его ИДЕНТИЧНЫМ СЕБЕ САМОМУ в разные моменты времени. А идентичность себе всех остальных объектов определять, сравнивая с эталоном по оговоренным признакам» [10, с.67]. Человек пытается преодолеть такую невозможность, меняя на протяжении эталоны. Например, эталон веса уже менялся на протяжении истории неоднократно – эталоном одного килограмма уже были и вес одного кубического дециметра воды при нулевой температуре и вес одного литра воды при четырёх градусах Цельсия и цилиндр из чистой платины, равный весу одного литра воды (поскольку водой как эталоном неудобно пользоваться) и наконец, был создан цилиндр из очень плотного платиноиридиевого сплава.
Всё вышесказанное предполагает фазовое пространство, связанное с обычным трёхмерным евклидовым пространством. Но если расширить фазовое пространство на всё пространство Минковского, то мы можем получить концепт, где сущность возвращается к собственным корням не только в пространстве координат и скоростей, но и во времени. Если вообразить, что слои могут перемешиваться, не нарушая очерёдности, то такая возможность появится. «Ключом к разгадке служили повторяющиеся операции растягивания и свёртывания фазового пространства – те самые, что имитируют действия кондитера, который раскатывает тесто для пирожных, складывает его, затем, вновь раскатав, опять складывает, формируя таким образом хрупкую многослойную структуру» [7, с. 193]. Попытка изображения подобного представления дана на рис.2.
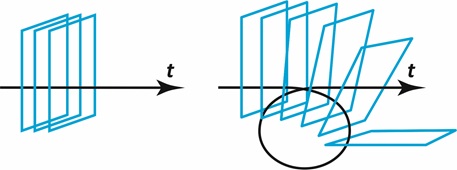
Рис. 2
Из диаграммы видно, что в некоторый момент всё-таки происходит нарушение причинно-следственных связей, когда цикл соединяется с предыдущим линейным участком, и, возможно, именно в такие моменты уплотнения фазового пространства происходит событие. Действительно ли события несут скорее несчастья, чем благо? Нет, это не так, ибо речь идёт о двойной структуре каждого события» [8, с. 198]. Двойственность, образуемая при уплотнении, перекликается с двойственностью Делёза, поскольку событие – это всегда попытка фазировать, сделать когерентными два процесса, например, бытие индивида и бытие социального во время войны.
История в лицах
Для лучшего понимания дальнейшего попробуем развернуть эволюцию представлений о времени и выстроить некоторую логику. Нелогичность, парадоксальность понятия времени выразил святой Августин: «что же такое время? Если никто меня об этом не спрашивает я знаю, что такое время; если бы я захотел объяснить спрашивающему – нет, не знаю» [1, с.167]. И объяснение этого, в первую очередь, в том, что мы наблюдаем только проекции времени на момент теперь. Практически невозможно объять всё время в целокупности, так же как очень сложно представить объекты четырёхмерного пространства, которые изображаются в нашем мире в виде проекции на трёхмерие. И именно так проясняется недоумение от ограниченности Бога, замеченное Августином: «если же у Бога возникает новое деятельное желание создать существо, которое никогда раньше Им создано не было, то что это за вечность, в которой рождается желание, раньше не бывшее» [1, с.165]. Виктор Франкл в книге «Человек в поисках смысла» [16] называл такой парадокс димензиальной недостаточностью– проекция из пространства с большей размерностью в меньшую всегда что-то теряет – Бог содержит в себе не только всё пространство, но и время тоже. То, что человек наблюдает как разворачивание пространства во времени или, в предыдущих терминах, как расслоение пространства вдоль координаты времени, Бог наблюдает одновременно. «То, что человек схватывает как прошлое и будущее, Бог проживает в своём вечном настоящем. Бог – это Хронос: божественное настоящее – полный цикл, тогда как прошлое и будущее – измерение отдельного фрагмента цикла, вырванного из единого целого» [8, с. 197]. Таким образом пространство в котором проявляется Бог равно минимум четырём.
Как уже упоминалось, огромный вклад в представление о времени сделали античные философы. Мир воспринимался греками не в категориях изменения и развития, а как пребывание в покое или вращение в великом кругу. Тогда единое можно соотнести с Хроносом– временем сплошного настоящего, распространяющегося бесконечно в прошлое и будущее, замкнутого самого на себя (подобно нашей вселенной, которая как считается в космологии, бесконечна, но ограничена). «В Хроносе настоящее некоторым образом телесно. Настоящее – это время смесей и сочетаний, это сами процессы смешивания» [8, с. 213]. Такой круг был разорван христианством и появилась прямая: прошлое, настоящее и будущее, отмеряемое от рождения Христа. Такое время стоики называли Эоном: «если Хронос ограничен и бесконечен, то Эон безграничен как будущее и прошлое, но конечен как мгновение» [8, с. 217]. Пользуясь терминологией из физики можно представить себе эти два времени как объём и поверхность – если ограниченный объём попробовать как тесто раскатать в тонкий лист, то последний получится безграничной поверхностью. «Существенное различие проходит теперь не просто между Хроносом и Эоном, а между Эоном поверхностей и совокупностью Хроноса и умопомешательства глубины» [8, с. 213]. Попытка изобразить мысль Делёза представлена на рис.3, где красным обручем изображено сознание человека, сминающего Хронос, до момента теперь, и, таким образом, обнажая, его поверхность.
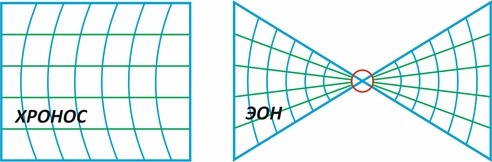
Рис. 3
Из рисунка видно, что при переходе к Эону ткань Хроноса сминается, образуя наложения друг на друга различных временных линий. Но так же, как в случае с жидкостью, которая, проходя через малое отверстие, меняет ламинарное движение на турбулентное, иначе говоря, эволюционирует, так и человек, сменив представления о времени, приобретает понимание концепта эволюции – человек в этой жизни должен так преобразоваться, чтобы стать достойным небесной жизни. Кроме того, подобная «турбулентность» демонстрирует сложность отношения понятий вдруг и теперь, обозначенную ещё Платоном.«Это „вдруг" видимо означает нечто такое, из чего происходит изменение в ту и другую сторону. В самом деле, изменение не происходит ни из покоя, пока это – покой, ни из движения, пока продолжается движение: но это странное по своей природе „вдруг" лежит между движением и покоем, находясь совершенно вне времени, а в него и из него изменяется движущееся, переходя к покою, и покоящееся, переходя в движение» [13, с. 69]. Для пояснения можно использовать образ запруды из которой торчит труба для перетекания воды: с одной стороны запруды, можно наблюдать болото, с другой стороны, обнаруживается турбулентная струя течения реки или ручья.
Можно представить иначе – образ ткани, которую пропускают через кольцо. Она может долго проходить насквозь без видимых проблем, но в некоторый момент из-за её роста складок образуется ком, который застревает в кольце, образуя затор. В этот момент теперь трансформируется во вдруг. «Линия Эона пробегается вышеуказанным «Вдруг», которое непрестанно перемещается вдоль этой линии и всегда испытывает нехватку собственного места» [8, с. 219]. Нехватка места здесь образуется по причине того, что быстрая и неаккуратная «укладка времени» приводит к сингулярности.
Следующим периодом, когда активно обсуждалась природа времени, были эпохи Возрождения и Нового времени. Ньютон считал, что время и пространство сверхфизичны, абсолютны и неизменны, что вновь нас относит к понятию единого. Напротив, Лейбниц полагал, что время – это спекулятивная сущность, что её в действительности нет и она может появляться только в момент взаимодействия, тогда, когда происходят какие-либо отношения и изменения. «Позиция Лейбница разделялась Э. Махом, считавшим категории абсолютного пространства и времени бессмысленными, Лейбниц и Мах полагали, что в отсутствии тел не существует ни пространство, ни время» [5, с. 154]. Лейбниц и, впоследствии, Мах ввели понятие отношений, выстраивая реляционную парадигму, для которых, по их мнению, понятие времени излишне – эти отношения происходят мгновенно. Одновременно теряется и понятие расстояния. Но тут создаётся ощущение неполноты: какой момент считать началом взаимодействия и, соответственно, появлением времени? Собственно из мгновенности отношений сразу следует, что эти отношения происходятнепрерывно, но тогда пространство и время присутствуют также непрерывно.
Ещё более сложный концепт времени был создан Иммануилом Кантом. Он, в некотором смысле, произвёл инверсию абсолютного времени Нъютона, поместив его внутрь субъекта, и сделав его априорно содержащимся внутри сознания. Он соединил идею абсолютности Ньютона и идею субъективности Лейбница, говоря, что время – есть форма внутреннего чувства. «Бесконечность времени означает не что иное, как то, что всякая определённая величина времени возможна только путём ограничений одного, лежащего в основе времени» [9, с. 72]. Но, с одной стороны, поверяя все текущие процессы течением реки, может создаться иллюзия о том, что река бесконечна. Кант подразумевает, что субъект поверяет все внешние феномены тем, что мы можем назвать внутренним временем. От такой точки зрения до идеи, что время у каждой сущности индивидуальное, и, что она согласовывает его с внешним временем, один шаг.
Гуссерль развил подход индивидуального времени, определив такие понятия как интенция (текущее восприятие объекта), ретенция – (идея первичной памяти или «послевкусие перцепции»), которая растягивает точку теперь в некоторый объём, удерживая ближайший контекст, сопровождающий восприятие объекта и протенция, ожидание ближайшего будущего. Важно, что время становится не совсем линейным, поскольку прошлое и будущее начинают влиять на момент теперь. Но и подход Канта и подход Гуссерля, несмотря на внесённую сложность локального времени, в глобальном плане, остаются на платформе ньютоновского концепта о гомогенном времени и отсутствии эволюции.
В общее прямолинейное течение мышления в девятнадцатом веке внёс сумятицу Ницше со своей идеей вечного возвращения равного. Она вновь относит нас к рисункам 1 и 2, что заметил Хайдеггер в своих лекциях о метафизике, где он пишет, что Ницше в связи со своим концептом ставит два вопроса. Во-первых, о цикличности времени: «что представляется нам двумя расходящимися прямыми дорогами, в действительности является лишь видимым отрезком гигантского круга» [17, с. 100]. Т.е. прямая вовсе не прямая, а гигантский круг, кривизна которого настолько мала, что мы не замечаем этого. Подобным образом древние не замечали кривизны земли и предполагали, что Земля плоская.
Смена парадигм мышления или эпистем, как говорил Фуко, изображена на рис. 4, где маленьким красным кругом показана идея античной цикличности, которая была разорвана христианством и превращена в голубую прямую, демонстрирующую соединение прошлого, настоящего и будущего в концепте времени Эона, и которую, в свою очередь, Ницше замкнул вновь в большом круге, что изображено чёрным. Чёрный цвет символизирует всю сложность и трагичность подобной мысли, которую пытался передать вслед за Ницше Хайдеггер, предполагая, что её не сможет понять последний человек, являющийся тоже концептом Ницше.
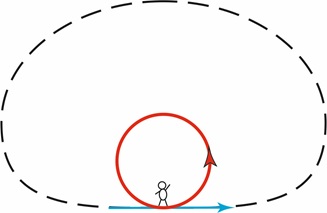
Рис. 4
Вторая часть идеи вечного возвращения равного затрагивает ограниченность фазового пространства или, иными словами, ограниченность единого, внутри которого трансформируется сущность, что показано на рис.1: «что только может существовать, уже должно было некогда существовать, поскольку за бесконечное время длительность существования конечного мира по необходимости должна была исчерпываться» [17, с. 102]. На рис. 1 видно, что цикличность нужно рассматривать шире, чем просто окружность. Цикличность – это возможность топологически сложной, замкнутой кривой в своей бесконечной эволюции. Само слово равного из мысли Ницше о вечном возвращении равного вновь относит нас к идеям Лиувилля и Пуанкаре о сохранении фазового объёма. Интересно, что и Ницше, и Пуанкаре жили в одно время и могли видеть работы друг друга. Представление о гигантском круге коррелирует с современным космологическим взглядом на возможную цикличность Больших взрывов.
Идея вечного возвращения равного при помощи рис.5 демонстрирует ещё одну важную мысль Ницше, что мгновение содержит в себе и прошлое и будущее, что вновь относит нас к концепту времени Хроноса. Тогда мгновение становится становящимся, иными словами, оно бытийствует. На рис. 5 показана центральная идея проективной геометрии (которая заняла очень важное место в современной математике), где каждая точка отождествляется с прямой (точка A с проходящей через неё голубой прямой). На рис. 5 круг времени из точки M (мгновение) при помощи голубых прямых проецируется на прямую времени и произвольной точке круга A ставится в соответствие точка прямой A'. И как несложно заметить, единственная точка M проецируется сразу в три точки: в точку теперь M' и точки +∞ и -∞, поэтому M=(+∞)+(-∞)+M', что подтверждает мысль Ницше.
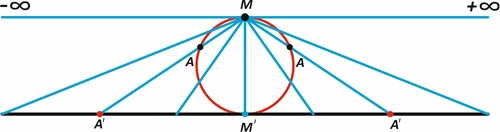
Рис. 5
Следующий существенный шаг в понимании времени сделал Бергсон, который раскрыл понятие длительности. Он говорил, что время – это не просто отрезок между событиями A и B, а что-то, что может содержать сингулярность в собственной длительности, которую он называл творческим порывом, который может быть незаметным в длительности, но существенно проявиться позже в новом содержании. «Переход представляет собой нечто большее, чем ряд состояний, т.е. возможных разрезов» [4, с. 117]. В противном случае будущее было бы предопределено, и художник, подступаясь к холсту, был бы вынужден нарисовать совершенно конкретную картину. Но будущее, вторгаясь в настоящее, как это предположено на рис. 2, и уплотняя его, преобразует момент теперь. Как показали работы по фрактальности времени возвращения Пуанкаре, внутри длительности содержатся мгновения, существенно влияющие на будущее: «недостатком данного подхода (традиционного) является то, что при этом не учитываются множества нулевоймеры» [3, с. 18] и неучтённое множество нулевой меры может оказаться очень значительным в смысле топологической энтропии или размерности» [3, с. 18]. Мгновение (или сумма мгновений) внутри длительности – это точка или множество нулевой меры, поскольку размер точки равен нулю (сумма нулей равна нулю), при этом мгновение влияет ключевым образом на размерность системы. Дальше мы разовьём этот концепт, рис. 6.
Ещё одна важная мысль Бергсона заключается в соотношении интуиции и интеллекта. Мы знаем, что в пространстве Минковского произвольный вектор имеет четыре координаты: одну временную и три пространственные. Тогда, следуя Бергсону, мы можем разложить функцию мышления тоже по четырём координатам: три пространственных координаты интеллекта и одну временную координату интуиции. «Наш интеллект ясно представляет себе только неподвижное» [4, с. 117]. Постижение сущности, как более геометрического представления, связано с интеллектом, тогда как понимание бытия, как эволюционирующего состояния, с интуицией (Бергсон по сути отождествлял интуицию и инстинкт). Именно интуиция вкладывает в момент теперь будущее и прошлое, замыкая большой круг, в соответствии с формулой M=(+∞)+(-∞)+M'.
Кинематографический метод о котором пишет Бергсон, и которым пользуется наука, разворачивающий момент за моментом всю длительность от точки A до точки B, возможен тогда, когда функция мышления раскладывается в произведение ортогональных осей пространства и времени , поскольку тогда мы можем исследовать время и пространство независимо. Если же такое невозможно, то в очерёдность моментов проявления сущности в пространстве постоянно вторгается координата времени, внося творческую составляющую, образуя «складки», что мы увидим дальше.
Какая размерность у времени?
Идея многомерного времени уже высказывалась. Например, авиаконструктор Роберто Бартини, бывший некоторое время руководителем С. П. Королёва, предложил концепт объёмного времени. Он считал, что реальность не описывается четырёхмерным пространством Минковского, а имеет размерность, равную шести: три пространственных координаты, и три – времени. Свидетельств в пользу трёхмерности времени Бартини приводит несколько, например, обнаруженная в физике симметрия между пространством и временем, выражающаяся в известной эргодической теореме, о подобии поведения множества частиц в один момент и одной частицы во множестве моментов. Бартини писал, что «Шестимерную протяжённость можно рассматривать как топологическое произведение двух нечётномерных протяжённостей одинаковой размерности и противоположной ориентации, вложенных друг в друга» [11].
Сложность принятия такой конструкции ещё заключается в том, что физики не пришли к единому мнению о размерности даже пространства. Здесь и работа математика Теодора Калуцы, с его пятимерием, где пятая координата свёрнута и имеет планковский размер, поэтому мы не замечаем её. Здесь и теория струн, где размерность пространства-времени равна десяти. Роджер Пенроуз критиковал высокую размерность: «я не могу всерьёз воспринимать её как заслуживающую внимания физическую модель» [12, с. 52]. Его критика была связана с понятием функциональной свободы – даже если дополнительная размерность имеет микроскопический размер, она порождает дополнительную свободу для появления и исчезновения полей, являющихся основой для описания современной физики.
Можно выдвинуть гипотезу, что размерность нашего пространства-времени когда-то была значительно больше, но в процессе эволюции она приобрела свой минимум: 4 (как у Минковского) или 6 (как у Бартини). «Максимальное значение объема протяженности образования имеет место при n = ±6, следовательно, наиболее вероятное и наименее невероятное, экстремальное, распределение элементарных образов объекта А соответствует 6-мерной конфигурации» [11]. Для нашего дальнейшего построения не является принципиальным равна ли размерность времени двум или трём, поскольку замкнутые кривые можно построить и в том и другом случае.
В разделе история в лицах мы не упомянули Гегеля по простой причине, что построение как минимум двумерности времени мы начнём, отталкиваясь от его диалектики. На наш взгляд, Гегель во многом определил онтологию движения, которая в свою очередь, определяет онтологию времени, поскольку время связано с понятиями изменчивости и постоянства. Гегель подробно пишет в «Науке логики»о становлении сущности, посредством внутренней диалектики: сущность отвергает саму себя и через постепенное снятие, проделывает полный диалектический круг, становясь снова собой. «Явление – это существующее, опосредованное своим отрицанием, которое составляет его устойчивость» [6, с. 532]. Он вводит понятия меры, неразличимости и т.д. Действительно, движущийся объект, с одной стороны, неразличим, он тождественен самому себе и занимает всё тот же фазовый объём, с другой стороны, различима разность его положений или мера расстояния. Мы не будем здесь подробно разбирать диалектику становления, поскольку это занимает многостраничный труд у самого Гегеля. Скажем только несколько комментариев.
Как мы знаем, диалектический цикл всегда замкнут (точнее говоря, почти замкнут в соответствии с временем возвращения Пуанкаре), напротив, прямолинейное движение нам таковым не кажется. Представим себе один из диалектических циклов: зерно-стебель-цветок-зерно. Он замкнут, т.е. в некотором смысле, он круговой (не совсем, поскольку в новом зерне имеются генетические изменения). Но представим любую из стадий, например, стадию роста стебля. Это прямолинейное движение вверх, задаваемое импульсом, сообщаемым растению солнцем. И нам может показаться, что такое движение будет длиться бесконечно. Но диссипация останавливает его. Точно также диссипация останавливает прямолинейное движение любого объекта. В конечном итоге любая сущность, оказывается в пределах стартовой точки – машина оказывается вечером в гараже, а капля воды, посредством цикла: дождь-ручей-река-море-облако-дождь, возвращается к началу в согласии с временем возвращения Пуанкаре.
Для понимания времени важны вопросы: что есть местоположение, что есть движение и что есть скорость, поскольку мы определяем время как , где s – путь, а v – скорость. Но в современной интерпретации лагранжева формализма и формализма квантовой механики координаты и импульсы являются независимыми сущностями, диалектика которых,по-видимому,и определяет движение объекта. По причине их независимости координата и импульс не коммутируют. Некоммутируемость означает, что движение туда и обратно по прямой невозможно, что всегда возникает цикл, который содержит в себе ненулевой сдвиг (эмерджентность). Подобная независимость приводит к принципу неопределённости, который в частном случае квантовой механики называется принципом неопределённости Гейзенберга. Таким образом, движение есть диалектика двух противоположностей: координат (постоянства) и скоростей (движения) и любая сущность находится поочерёдно: то в покое, когда мы можем померить её месторасположение, то в движении, когда мы можем измерить скорость. Именно димензиальной недостаточностью, т.е. редукцией шестимерного пространства координат-скоростей до трёхмерного пространства координат объясняется известная апория Зенона с покоящейся стрелой. «С появлением представления о скорости, которое не выводится целиком из представления о координате, а имеет собственную онтологию, остановка стрелы стала невозможна» [15, с. 65].
Но подобную онтологию можно представить и иначе, как нам кажется более развёрнуто, на рис. 6., где время как минимум двумерно, а момент покоя заменяется временной петлёй в согласии с рис. 2. Иными словами, то, что мы воспринимаем покоем – является диалектической петлёй во втором временном измерении, недоступном перцепции. Здесь красным изображён путь как мы его воспринимаем, а чёрным – реальный путь в пятимерном пространстве-времени.
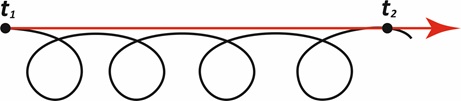
Рис. 6
Для лучшего прояснения сказанного воспользуемся образом работы квантового компьютера на рис. 7, для демонстрации мышления как движения сущности мысли субъекта. У такого движения также есть отрезки пути, которые могут восприниматься как линейные, но в итоге мысль всегда диалектически выстраивается в спираль, что показал Людвиг Витгенштейн – логика выстраивается на отрицаниях.
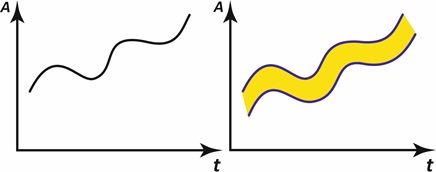
Рис. 7
На первой диаграмме рис.7. изображена работа обычного компьютера, основанная на традиционной аристотелевской логике исключённого третьего. Программист задаёт последовательность логических действий, что выражается в алгоритме решения задачи. В процессе её решения появляется график зависимости амплитуды (например, роста количества вируса) от времени.
В отличие от обычного компьютера, индивид, как и квантовый компьютер, не детерминирован, он находится в суперпозиции нескольких возможных алгоритмов (путей), и поэтому его график решения изображённа второй диаграмме рис. 7. в виде некоторой полосы. Иначе говоря, на решении сказывается принцип неопределённости (например, между вирусом и температурой среды), в результате чего решение начинает расплываться. Теоретически можно сказать, что ширина этой полосы бесконечна (решение задачи имеются и за её пределами), но,как это принято в физике, её можно ограничить наиболее вероятным решением задачи, определив вероятностьравной, например, не меньше 0,5. И, соответственно, можно сказать, что данная полоса — это движение максимально вероятного решения задачи (мы можем на полпути в садик забыть ребёнка на скамейке, но с большой долей вероятности мы доведём его до садика тем или иным образом). Такая движущаяся «клякса», превратившись из одномерной в двумерную структуру, может решать в континуальном развертывании более сложные задачи, чем традиционный алгоритм, основанный на логике Аристотеля. Иными словами, такой алгоритм, формирующий решение, может обогнуть состояние классического алгоритма с отсутствующим решением за счёт суперпозиции (волновой, диалектической природы). Таким образом, само окружающее пространство помогает решить поставленную задачу.
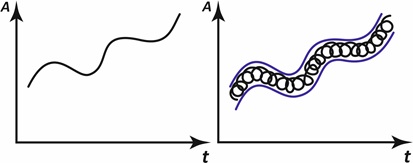
Рис.8
Если соединить рисунки 6 и 7, то можно обнаружить диаграмму времени как негации вечности, показанную на рис. 8. На первой диаграмме время изображено как параметр, принятый в традиционной физике и математике (ньютоново, абсолютное время), где мы видим некоторую кривую (функцию) зависимости чего-либо от времени, структурно отображающую аристотелевскую логику, где последующая точка кривой, чётко следует из предыдущей точки, согласно некоторому алгоритму (например, камень падает согласно алгоритму, определённому тяготением, и, соответственно, теорией, его описывающей). В отличие от этого, диалектическое движение будет представлять из себя некоторую двумерную спираль, расплывшуюся «кляксу», движущуюся вдоль кривой, подобной первой. Например, бросая камень, при заданных начальных условиях, в случае классического алгоритма, мы получим прохождение через единственную точку на определённой высоте, и при промахе задача остаётся нерешённой, в случае гегелевского алгоритма, камень «заметает» собой некоторую пространственно-временную ширину, поражая цель.
В подтверждение спиральной онтологии движения можно сослаться на работу Сергея Сипарова [14]. Она посвящена тому, что все поля (гравитационное, электромагнитное и т. д.) можно представить как пространственные эффекты, по аналогии с представлением Эйнштейна о гравитации как искривлении пространства. Он обнаружил, что если предположить, что метрический тензор, введённый Эйнштейном и определяющий свойства пространства, зависит не только от координат (от места, где его вычисляют), но и от скорости объекта, то оказывается, чтообъект движется не по прямой, а по спирали, если быть точнее, то по спирали, навитой на искривленный цилиндр. Подобное спиралевидное движение он рассматривал в микромире, сопоставляя его с описанием движения в квантовой механике и показал их идентичность. Но в макрофизике мы не замечаем, чтобы тела двигались по спирали.
Разрешением парадокса является то, что сущность движется по спирали во времени. Время перестаёт быть некой прямой, формирующей причинно-следственные связи. Вместо этого время становится фактором, эксплицирующим реальность из множества пространственных возможностей, укладывающихся в размер «кляксы». Подобное представление напоминает шов портного: когда иголка делает шаг вперёд, полшага назад. Но эти полшага назад, иными словами, петля имеют не пространственный, как мы привыкли,а временной вид, он делается назад в прошлое.Скорее всего и шаг вперёд делается с запасом – петля «заметает» сколько-то из будущего. «Сегодня большинство исследователей уверено в принципиальной многоликости времени. Верны многие модели, каждая в своей области, где она работает лучше других. Даже поворот во времени разрешили элементарным частицам в малых масштабах, с последующим возвратом на путь истинный, то есть в будущее, как все…» [10]. Такая картина соответствует единству гуссерлевских интенции, ретенции и протенции в синтезе точки теперь.
Структуру типа петли лучше описывать комплексным числом, рис. 9. Напомним, что комплексное число принадлежит не прямой, а плоскости и определяется двумя параметрами: либо двумя числами, которые соответствуют проекциям комплексного числа на оси x и y – a иb, либо амплитудой и фазой . Существенно, на что обратил в своей работе Сипаров [14], что каждой сущности в его представлении соответствует некоторая фаза φ, что также согласуется с нами.
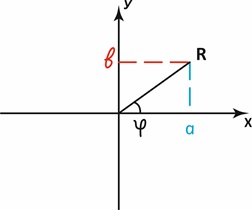
Рис. 9
В традиционной квантовой механике волновая функция частицы описывает зависимость от времени как , где фаза φ= одномерна и линейно зависит от времени и энергии. На рис. 9 хорошо виден основной парадокс квантовой механики: коллапс волновой функции. Если представить ось x, как прибор, который измеряет некий параметр частицы, то проекция волновой функции на эту ось a будет разной в разные моменты времени, но всегда меньшей R, что в квантовой механике проясняется вероятностью, а в нашей интерпретации – димензиальной недостаточностью (нехваткой размерности, иными словами, наблюдается только «тень», проекция более многомерного объекта в пространство с меньшей размерностью.
В нашем представлении сущность, двигаясь по замкнутой кривой внутри временного многообразия, выбирает подходящее пространственное решение и эксплицирует его в реальность. Она осциллирует, взаимодействуя с вечностью, то возвращается в прошлое, будто припоминая что-то, то вновь устремляется в будущее. И благодаря этому припоминанию время соединяет прошлое и будущее не только локально, но и образуя дальние связи. Можно сказать, что благодаря такому взгляду на время эксплицируется память материи и её потенциальность. На рис. 10 изображены возможные пространственные решения в виде ежа и время в виде окружности с единственным разрывом, эксплицирующим реальность, который можно назвать моментом теперь. Эту диаграмму можно назвать воротами времени.
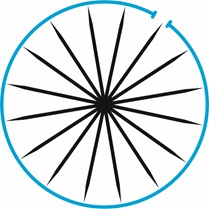
Рис. 10
Тогда не обязательно, что в следующий момент временной разрыв должен быть строго напротив предыдущего, что изображено на рис. 11, где голубыми окружностями изображена последовательность временных слоёв. Строгая траектория пространственных решений приобретает расплывчатый вид. И таким образом, проясняются принцип неопределённости Гейзенберга и представление Бергсона о творческой эволюции – если эти разрывы будут дальше друг от друга, то это будет восприниматься как иррациональное творчество.
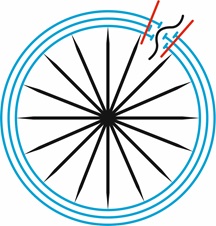
Рис. 11
Кроме того, такая диаграмма проясняет парадокс Эверетта, который предложил многомировую интерпретацию квантовой механики. Если в обычной трактовке описывается вероятность некоторого состояния, реализующаяся в каком-то одном виде, то в эвереттовской эти состояния реализуются одновременно, т.е. происходит расслоение реального мира на континуум миров. В одной вселенной вы – удачливый игрок, во второй – незначительный клерк. Если у Эверетта параллельно существует континуум вселенных, то в нашем описании время отсеивает их, оставляя, с одной стороны, единственную, с другой стороны, у всех есть возможность поучаствовать в этой единственности, и, соответственно, остаётся вселенная, реализующая все эти многомерные возможности. Такое представление о времени коррелирует с гегелевским представлением, где время рассматривается в качестве негации вечности, которая очевидно содержит весь континуум вселенных. Время как отрицательный момент вечности выбирает одну единственную вселенную.
В подтверждение существования петель времени, хотелось бы добавить несколько слов о теории динамических систем, которая активно развивается последние шестьдесят лет, изучая хаос, пытаясь его упорядочить. Она началась с обнаружения Лоренцем невозможности длительного прогноза в погоде, поскольку малые отклонения в начале приводят к экспоненциальному росту изменений во времени, что приобрело название эффект бабочки. Одним из ярчайших достижений этой теории было изучение итерационного уравненияxj+1 = rxj(1 – xj), которое демонстрирует множество физических процессов,например, ежегодный прирост количества кроликов на ферме, здесь xj и xj+1 – количество кроликов в предыдущий и текущий год. Подобные уравнения, как и вся теория динамических систем, строятся на предположении, что можно не изучать промежутки времени между цикличными моментами, иссекая их. Но эта же идея содержится и в нашем концепте времени, где кажущаяся прямая времени расслаивается на множество петель, которые мы не замечаем.
В заключение скажем ещё об одном физическом эффекте, с которым связывают понятие времени, об энтропии. Например, Стивен Хокинг указывал на стрелу времени, которая определяется увеличением энтропии и достижением её максимума, поскольку состояний хаоса гораздо больше, чем состояний порядка и, соответственно, они более вероятны, и «чтобы объяснить, почему разбитые чашки никогда не возвращаются целыми обратно на стол, обычно ссылаются на то, что это противоречило бы второму закону термодинамики» [18, с. 180]. На наш взгляд, одномерное время – можно назвать статистическим временем, т.е. усреднённым по множеству элементов (атомов газа в сосуде, членов партии, звёзд в галактике и т.д.). Но Пригожин обратил внимание на закон сохранения фазового объёма и на то, что параллельно с распадом всегда происходят процессы самоорганизации. Разница лишь в том, что распад происходит непрерывно, а самоорганизация (через бифуркацию) – сингулярно или точечно в согласии с нашим концептом, в момент замыкания петливремени. Но такое время нужно назвать, в противовес статистической стреле времени, временем индивидуальным.
Литература
- Августин А. Исповедь. / А. Августин. – М.: Республика, 1992. – 335 с. – Текст : непосредственный.
- Арнольд В. И. Математические методы классической механики. / В. И. Арнольд. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 472 с. – Текст : непосредственный.
- Афраймович В. Угальде Э. Уриас Х. Фрактальные размерности для времён возвращения Пуанкаре. / В. Афраймович, Э. Угальде, Х. Уриас. – Ижевск: НИЦ «Регулярная и хаотическая динамика», Ижевский институт компьютерных исследований, 2011. – 292 с.– Текст : непосредственный.
- Бергсон А. Творческая эволюция. / А. Бергсон. – М.: Академический проект, 2015. – 320 с. – Текст : непосредственный.
- Владимиров Ю. С. Реляционные основания физики и метафизики / Ю. С. Владимиров. – Текст : непосредственный. // Метафизика. Век ⅩⅩⅠ. Альманах. выпуск 2: сборник статей/ под ред. Ю. С. Владимирова. БИНОМ. Лаборатория знаний, Москва,2007, С.150-204.
- Гегель Г. В. Ф. Наука логики. / Г. В. Ф. Гегель. – М.: Издательство АСТ, 2019. – 912 с.– Текст : непосредственный.
- Глик Д. Хаос. Создание новой науки. / Д. Глик. – М.: Издательство АСТ: CORPUS, 2022. – 432 с.– Текст : непосредственный.
- Делёз Ж. Логика смысла. / Ж. Делёз. – М.: Академический проект, 2015. – 472 с.– Текст : непосредственный.
- Кант И. Критика чистого разума. / И. Кант. – М.: Эксмо, 2015. – 736 с.– Текст : непосредственный.
- Коганов А. В. Время как объект науки / А. В. Коганов. – Текст : непосредственный. // Мир измерений, № 2-3, 2002, С. 18-22.
- Никитин А. П. Объёмное время Бартини / А. П. Никитин. – Текст : непосредственный.// Проблемы исследования вселенной, № 39(2), 2020, С. 174-195.
- Пенроуз Р. Мода, вера, фантазия и новая физика Вселенной. / Р. Пенроуз. – СПб.: Питер, 2020. – 512 с.– Текст : непосредственный.
- Платон Парменид. / Платон. – Текст :электронный // plato.spbu.ru: [сайт]. – 2017. – 27 июля. – URL: https://www.plato.spbu.ru/TEXTS/PLATO/Academia/004-01.pdf (дата обращения 02.02.2022)
- Сипаров С. В. Геометрические аспекты квантовой механики / С. В. Сипаров. – Текст :электронный // ютубканал – 2017. – 27 июля. – URL:https://www.youtube.com/watch?v=vufZcOfQ4aE&t=1148s (дата обращения 10.02.2022)
- Стригин М. Б. Логика логики Гегеля или начала квантовой механики / М. Б. Стригин. – Текст : непосредственный // Вестник РХГА. 2020. №4. С. 64–82.
- Франкл В. Человек в поисках смысла. / В. Франкл. – М.: Прогресс, 1990. – 368 с. – Текст : непосредственный.
- Хайдеггер М. Лекции о метафизике. / М. Хайдеггер. М.: Языки славянских культур, 2010. – 160 с.
- Хокинг С. Краткая история времени: От большого взрыва до чёрных дыр. / С. Хокинг. – СПб.: ООО «Торгово-издательский дом «Амфора», 2015. – 223 с.– Текст : непосредственный.
Strigin M. B. Chelyabinsk, PhD, Director of Mitrial LLC, strigin1969@gmail.com
Negation of Eternity or Gate of Time
The paper proposes to combine the concept of resting, circular, oscillating time of Parmenides, which leaves being in the global sense unchanged, and the concept of linear time of Heraclitus, which has a past, present and future, into their superposition, which in the first approximation can be figuratively represented as a spiral figure. But if the spiral is a simple sum of two movements – rotational and translational, then the superposition assumes a more complex combination of them, depending on the phase of oscillating time. Such an examination makes it possible to clarify such concepts and paradoxes as emergence, which is an explication of a new quality, Bergson's duration, Hegel's concept of time as negation of eternity, and, finally, one of the most exotic paradoxes of modernity – Everett's multi-world interpretation of quantum mechanics. To clarify this consideration, the principle of least action and the theory called the Poincare return time will be involved.
Key words: time, dialectics, quantum mechanics, coordinate, velocity, evolution, Everett, Poincaré return time, phase space.
References
- Augustin, A. (1992). Ispoved [Confession]. Republic, Moskow, 335 p. (inRuss.)
- Arnold, V.I. (1989). Matematicheskiye metody klassicheskoy mekhaniki [Mathematical methods of classical mechanics]. Nauka, Gl. ed. phys.-mat. lit., Moskow, 472 p. (inRuss.)
- Afraimovich, V., Ugalde, E. and Urias, H. (2011). Fraktalnyye razmernosti dlya vremen vozvrashcheniya Puankare [Fractal dimensions for Poincare return times]. SIC "Regular and Chaotic dynamics", Izhevsk Institute of Computer Research, Izhevsk, - 292 p. (inRuss.)
- Bergson, A. (2015). Tvorcheskaya evolyutsiya [Creative evolution]. Academic Project, Moskow, 320 p. (inRuss.)
- Vladimirov, Yu.S. [2007]. Relyatsionnyye osnovaniya fiziki i metafizika [Relational foundations of physics and metaphysics] in Metaphysics. Century ⅩⅩⅠ. Almanac. Issue 2: collection of articles/ edited by Yu.S. Vladimirova. BINOMIAL. Laboratory of Knowledge, Moscow, , pp.150-204. (inRuss.)
- Hegel, G.V.F. [2019]. Nauka logiki [Science of Logic]. AST Publishing House, Moskow, 912 p. (inRuss.)
- Glick, D. Chaos. [2022]. Khaos. Sozdaniye novoy nauki [Creation of a new science]. AST Publishing House: CORPUS, Moskow, 432 p. (inRuss.)
- Deleuze, J. [2015]. Logika smysla [Logic of meaning]. Academic Project, Moskow, - 472 p. (inRuss.)
- Kant, I. [2015]. Kritika chistogo razuma [Criticism of pure reason]. Eksmo, Moskow, 736 p. (inRuss.)
- Koganov, A. V. [2002]. Vremya kak obyekt nauki [Time as the object of science], in The world of measurement, 2-3, pp. 18-22. (inRuss.)
- Nikitin, A. P. [2020]. Obyemnoye vremya Bartini [Volumetric time Bartini], in Problems of research of the universe, 39(2), pp. 174-195. (inRuss.)
- Penrose, R. [2020]. Moda. vera. fantaziya i novaya fizika Vselennoy [Тhe Fashion, faith, imagination and the new physics of the Universe]. St. Petersburg, - St. Petersburg, 512 p. (inRuss.)
- Plato [2017]. Parmenid [Parmenides], in plato.spbu.ru, available at: https://www.plato.spbu.ru/TEXTS/PLATO/Academia/004-01.pdf accessed 02.02.2022 (inRuss.)
- Siparov, S.V. [2017]. "Geometricheskiye aspekty kvantovoy mekhaniki" [Geometric aspects of quantum mechanics], in YouTube channel, available at: https://www.youtube.com/watch?v=vufZcOfQ4aE&t=1148s accessed 10.02.2022 (inRuss.)
- Strigin, M.B. [2020] Logika logiki Gegelya ili nachala kvantovoy mekhaniki [Logic of Hegel's logic or the beginnings of quantum mechanics], in Bulletin of the Russian Academy of Sciences, 4, pp. 64-82. (inRuss.)
- Frankl, V. [1990]. Chelovek v poiskakh smysla [Man in search of meaning]. Progress, Moskow, 368 p. (inRuss.)
- Heidegger, M. [2010]. Lektsii o metafizike [Lectures on metaphysics]. Languages of Slavic cultures, Moskow, 160 p. (inRuss.)
- Hawking, S. [2015] Kratkaya istoriya vremeni: Ot bolshogo vzryva do chernykh dyr [A brief history of time: From the big bang to black holes]. - St. Petersburg: LLC "Trade and Publishing House "Amphora", 223 p. (inRuss.)

