Аннотация. В данной работе эксплицируется феномен комплекснозначности бытия, проявляющийся в виде волновой онтологии. Такая онтология подразумевает, что любая сущность обладает, помимо амплитуды, иными словами, энергетического аспекта, ещё и фазой, которая отвечает за имплицитное взаимодействие сущностей, проявляющееся в виде интерференции. В традиционном подходе к исследованию сущности, имеющем статистический характер, индивидуальная фаза теряется, иными словами, любая наука: биология, социология, физика – изучает общее, принадлежащее большей части изучаемого множества. Показано, что комплексное число имеет максимальное значение когнитивности, которая сначала возрастает с ростом сложности числа: от натуральных чисел к комплексным, а затем падает к кватернионам и октавам. Показано, что традиционная наука «стесняется» понятия комплексного числа, считая его применимость узко ограниченной. Также продемонстрирована возможность комплексификации гуманитарных представлений, например, психоанализа.
Ключевые слова: комплексное число, модель, гносеология, диалектика, постоянная Планка, квантовая механика, волновая механика, экологическая ниша.
The complex meaning of being or wave ontology
Abstract. In this paper, the phenomenon of the complexity of being is explicated, which manifests itself in the form of wave ontology. Such an ontology implies that any entity has, in addition to the amplitude, in other words, the energy aspect, also a phase that is responsible for the implicit interaction of entities, manifested in the form of interference. In the traditional approach to the study of the essence, which has a statistical character, the inpidual phase is lost, in other words, any science – biology, sociology, physics - studies the general, belonging to the majority of the studied set. It is shown that a complex number has a maximum value of cognition, which first increases with increasing complexity of the number: from natural numbers to complex numbers, and then falls to quaternions and octaves. It is shown that traditional science is "shy" of the concept of a complex number, considering its applicability to be narrowly limited. The possibility of the complexification of humanitarian concepts, for example, psychoanalysis, is also demonstrated.
Keywords: complex number, model, epistemology, dialectics, Planck's constant, quantum mechanics, wave mechanics, ecological niche.
В данной работе предпринята попытка распространить понятие комплексного числа из области математики и физики в область гуманитарных науки; внести понимание, что бытие как вещей, так и символических форм наиболее полно описывается при помощи комплексных чисел. Больше двух тысячелетий считается, что мир описывается действительными числами, но был период, когда математический аппарат был ограничен целыми и рациональными числами, а иррациональные числа, которые, как оказалось, составляют большую часть действительных чисел, были скорее маргинальным понятием. «В «Законах» Платон признаётся, что ему неловко, что с идеей несоизмеримости длин и с иррациональными числами он познакомился сравнительно поздно, и сокрушается, что многие греки его поколения до сих пор о них не знают» [7, с. 105]. Вместе с пониманием иррациональных чисел пришло понимание акцидентальности бытия.
Теперь пришло время обобщить понятие комплексных чисел. Основная сложность здесь заключается в том, что с перцепцией действительных чисел мы встречаемся повсеместно (две кошки, полтора землекопа, число π), а комплексные числа имеют скорее имплицитный характер. С действительными числами связаны различные философские концепты, например, Платоновы тела или золотое сечение. Последнее встречается повсеместно, от микроскопических объектов в кристаллографии, до макрообъектов, типа галактик и т. д. и описывает, с одной стороны, предельную устойчивость, с другой стороны, масштабные переходы, порождающие фрактальность. Иррациональное число π символизирует диалектику и гармонию окружности, и, как будет видно ниже, связано с комплексными числами.
Попробуем продемонстрировать, что комплексные числа лежат в основе онтологии устойчивых состояний, которые позволяют, выражаясь словами Мамардашвили, «видеть нечто, а ни ничто»[8]. Если ещё недавно комплексные числа можно было обнаружить только в прикладных науках – квантовой механике, волновой физике, электродинамике и т. д., то теперь такие числа используются и в трансцендентальных концептах, например, во фрактале Мандельброта.
Путь от единичного (некоторого феномена) к абстрактному (к философской категории) всегда являлся основным путём философа, поскольку философия с её предельным уровнем абстракции изначально находила собственные образы в реальном. «Философские понятия вначале являются чувственными значениями, перенесёнными в духовную сферу, и что установление собственно абстрактного значения тесно связано со сглаживанием метафорического аспекта в первичном значении, а значит, с забвением этого значения, которое из собственного становится несобственным» [11, с. 231]. Можно сказать, что духовная сфера появилась как расслоение имманентного мира на два: на мир реальный и мир символических форм – семантическое пространство. И внутри семантического пространства идёт такая же эволюция, как и в объективном мире (семантические карты-науки расширяются). Человек, на что обратил внимание Декарт, является суммой (в современном контексте – суперпозицией) телесного и духовного, иными словами, он стоит одной ногой в объективном мире, а второй в семантическом, и подобно рыбаку ловит рыбу в море имманентного, а вытаскивает её на берег символического. Подобно такому рыбаку, мы возьмём образ комплексного числа из математики (которая является наиболее абстрактной наукой и, в некотором смысле, квинтэссенцией философии) и посредством волновой физики обобщим его на всё бытие.
Несмотря на предельную абстрактность, понятия математики также подвержены такому процессу, как дисперсия (расплывание), и поэтому были неоднократные попытки привести всю математику к единственному знаменателю, которые в основном провалились (программа геометризации Клейна, объединение математики группой Бурбаки, физикалистские попытки Карнапа), хотя благодаря им были обнаружены многие математические структуры. Математика всегда оказывается объёмнее, когнитивнее данных ей рамок, и подобно тесту «вылезает из собственной кастрюли». Поэтому процесс перетекания концептов из математики через физику в философию и обратно является перманентным.
Волновая парадигма
В нашей работе [14] была предложена модель нелинейного осциллятора, описывающая в общем виде бытие произвольной сущности, демонстрирующая волновую динамику между моментами синтеза, что показано на следующей диаграмме, где A – это амплитуда состояния сущности (например, злость человека или верифицируемость некоторой теории), а t – это время:
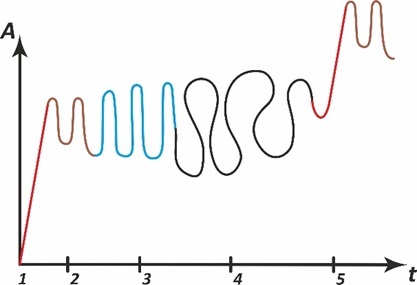
Данная диаграмма демонстрирует объединение всех трёх законов диалектики Гегеля. Она эксплицирует четыре основных этапа эволюции произвольной системы: 1 – этап синтеза сущности, 2 – этап адаптации (встраивания в существующий контекст, поскольку новая сущность «раздвигает» рамки бытия), 3 – гармонический этап (идеальное, исчерпавшее когнитивность, существование сущности), 4 – этап хаоса, заканчивающийся синтезом новой сущности– этапом 5. Несложно заметить, что первый этап отображает первый закон диалектики перехода количества в качество, второй и третий этапы демонстрируют законы взаимного проникновения противоположностей и закон отрицания отрицания (очередной полупериод отрицает предыдущий). Но данная диаграмма демонстрирует два новых аспекта, которых не было у Гегеля – этап синтеза всегда предваряется этапом хаоса, что характеризуется неустойчивостью существования, и наличествует этап адаптации 2. Этап хаоса 4 онтологически необходим, поскольку синтез, означающий преображение сущности, возможен только на таком этапе. Это напоминает движение велосипедиста, который может сделать крутой поворот, только притормозив велосипед, но в момент торможения руль вибрирует по причине хаотической неустойчивости движения велосипеда.
Можно несколько заинтриговать читателя предположением, что бытие определяется всего тремя иррациональными числами: определяющим пространство – иррациональным числом π, определяющим время или, что то же самое, непрерывную эволюцию иррациональным числом e, и определяющим сингулярную или скачкообразную эволюцию иррациональным числом золотого сечения φ, что прекрасно видно из диаграммы нелинейного осциллятора: число π определяет пространственные осцилляции сущности, число e определяет эволюцию амплитуды, или огибающую осцилляций, а число φ– сингулярный скачок в момент синтеза новой сущности, которая собирается из суммы предыдущего. Таким образом, сама диаграмма является верификацией подобного представления.
Несложно заметить, что эта диаграмма демонстрирует волновое (осциллирующее) поведение произвольной сущности, но для лучшего понимания такой онтологии необходимо обобщить термин волновая.
Дискуссия о корпускулярно-волновой дуальности материи началась ещё с работ Ньютона и Гюйгенса, но, главным образом, была инициирована в квантовой механике работами Джорджа Томсона и Де Бройля, после обнаружения в ходе двухщелевого эксперимента, что электроны, выпущенные из одной пушки и разделённые потом на два потока, интерферируют между собой. Иными словами, электроны ведут себя одновременно и как частицы материи, и как волны. Но помимо парадигмы, принявшей такой дуализм, основателями которой считаются Нильс Бор и Вернер Гейзенберг, была вторая, волновая парадигма Эрвина Шредингера, внутри которой пытались прояснить все эмпирические данные квантовой механики, включая свидетельства корпускулярности, не выходя за её рамки. Известно письмо Макса Борна Шредингеру с критикой его чисто волнового подхода. «Однако эта интерпретация была несогласованной, так как волновой пакет со временем расширяется, и в конечном итоге электрон должен будет занять всё доступное пространство» [10]. Многие парадоксы квантовой механики, (например, упомянутое расширение пакета, согласующееся с тем, что вращающийся с центробежным ускорением электрон должен излучать и, соответственно, падать на ядро), имеют волновое разрешение: как и в случае с солитоном (состоящим из определённого числа волновых мод, которые поочерёдно трансформируются друг в друга, не меняя их общего количества), моды, соответствующие собственным значениям электрона в атоме, могут переходить друг в друга, оставаясь внутри ограниченного пакета (нечто подобное в оптике называется самофокусировкой, когда одна нелинейность компенсируется другой). Иными словами, ускорение преобразует волновой пакет электрона, но сохраняет его в общем виде.
Следующим шагом волновой парадигмы можно считать теорию струн, которая пока является в большей степени математическим концептом, предполагающую, что в основе всего видимого лежат струны и браны, являющиеся волновыми объектами. Если классическая физика представляет объект точечным, нуль-мерным и, соответственно, его траектория в четырехмерном пространстве-времениявляется некоторой кривой, то в теории струн, элементарным объектом становится волна – одномерная кривая линия. И, соответственно, её траектория в четырехмерном пространстве-времени становится поверхностью. (Это несложно представить, любая кривая порождается движением точки, поверхность движением кривой, объём движением поверхности, что может описываться математическим термином расслоение). Но поверхность, по крайней мере локально, описывается при помощи римановой поверхности или комплексного одномерного пространства.
При мысли о волне человек представляет себе что-то типа морской или электромагнитной волн. Основное отличие волн от корпускул – в их энергетическом поведении: они обладают возможностями дифракции и интерференции, которая приводит к энергетическому пространственному перераспределению. Это несложно представить, вспомнив интерференционные полосы, образующиеся при взаимодействии двух когерентных лучей света, идущих от двух щелей (если две волны находятся в фазе, то они резонансно суммируются, если в противофазе, то они уничтожают друг друга). Внутри этих полос интенсивность света не в два раза больше, как если бы источники света просто накладывались друг на друга, но благодаря их взаимодействию больше в четыре раза. В случае, если источников света не два, а N, то интенсивность в интерференционных полосах N^2 , что больше в N раз, чем при простом сложении. Несложно представить интерференционный эффект, если интерферируют〖6,022×10〗^23 атомов, составляющих моль вещества.
Математика, которой пользуются в современных науках, основывается большей частью на действительных числах. В таком виде она является предельным уровнем абстракции, это уровень множественного, присущего всему сущему (два гриба, тридцать три звезды), на котором всё единичное гибнет. Напротив, интерференция, кратко описанная выше, использующая в собственном описании комплексные числа – это всегда уровень единичного, поскольку, чтобы можно было наблюдать интерференцию двух сущностей, они должны быть когерентны. Понятие когерентности фундировано понятием фазы, которое будет раскрыто ниже. Фаза, в отличие от амплитуды, может быть только индивидуальна. Когерентное состояние крайне сложно получить во множественном виде. Оно образуется в исключительных случаях, таких, как лазерное излучение или газовые космические мазеры (на самом деле когерентное состояние встречается не так уж и редко, например, состояние кристалла когерентно, о чём свидетельствует невозможность присоединения отпавшей, уже некогерентной части). В подобных случаях основная математическая парадигма теории множеств 2+2=4 нарушается, выше уже было показано, что в таких случаях, например, может быть 2+2=8. Такое положение никак не нарушает закон сохранения энергии, поскольку в случае когерентных взаимодействий происходит её перераспределение. Но математика не умеет производить действия типа 2+2=8, эксплицирующие резонансные эффекты, точнее говоря, умеет, но для этого необходимо онтологизировать комплексное число.
Для образного представления о фазе можно представить произвольную сущность в виде вектора (стрелки) с амплитудой A, быстро вращающуюся вокруг собственной оси (в квантовой механике используется понятие спина), тогда угол, образующийся при вращении, можно назвать фазой. Это показано на диаграмме.
Одним из ярких примеров подобной иерархии, определяющей ряд Тейлора, является соотношение понятий желания и требования в психоанализе. Еслитребование, как его определял Лакан, всегда прозрачно и действует по прямой, то желание, напротив «скрыто за углом» [3].Если первое имеет скорее геометрические основания, поскольку связано всегда с намерением получить что-то конкретное, то второе в большей мере динамично – желание гораздо сложнее артикулировать.
Аналогичную картину можно обнаружить при изучении социального: в первую очередь наблюдаются непосредственные причинно-следственные связи, а затем, исходя из них, выстраивается теория. Так выстраивал свою теорию социального Макиавелли, который обосновывал поведение индивидов, отталкиваясь от страстей, присущих каждому из них. Такое описание является следствием логики первого порядка, являющейся первым членом ряда Тейлора функции мышления. Того же порядкасоциальная когерентностьв описании Фрейда:он приписывал каждому субъекту понятие либидо, определяющее влечение индивида по отношению к лидеру социальной группы (так до конца не определив понятие либидо) [15]. И тот, и другой, очевидно, правы, если учитывать только первый член ряда функции мышления. Но, например, представление о групповой солидарности, названной Ибн Халдуном асабией, вряд ли можно описать, исходя только из индивидуального поведения субъекта (например, либидо). Очевидно, что этот процесс имеет более высокий уровень сложности, для описания которого необходимо учитывать не только индивида и его ближайшее окружение, но и всю социальную иерархию, что вновь заставляет учесть динамические аспекты феномена. И каждый следующий член ряда Тейлора вносит свой, пусть и малый, вклад в бытие индивида, который уже не может рассматриваться как единичное (как константа, определяющая первый член ряда), но как часть когерентного социального, ставшего единичным на более высоком уровне.
Поскольку представление о ряде Тейлора использует понятие расстояния между точками пространства, в котором определена исследуемая функция, то для нахождения разложения функции мышленияв подобный ряд необходимо ввести метрику в семантическом пространстве. Но такая метрика, хотя и математически некорректна, уже существует – геометрию знания (отношение наук друг с другом) описывает эпистемология, динамические характеристики задаются гносеологией. Для более чёткого определения можно обратится к дескриптивной лингвистике [5], где «расстояние» между словами определяется как частота их совместного использования. С одной стороны, появляется вполне конкретная метрика, с другой стороны, она учитывает только статистические аспекты и слабо учитывает семантические аспекты. Кроме того, подобная метрика очевидно эволюционирует – если семантическое «расстояние» между словами время и деньги, согласно дескриптивной лингвистике, до ⅩⅩ века было большим, поскольку эти слова вряд ли использовались совместно, то на современном этапе появление поговорки «время-деньги» существенно сократило дистанцию между ними.
Попробуем представить функцию мышления, которую также можно назвать функцией теперь, в виде убывающего ряда последовательности перцепций и актов воображения. T=f(P1)+f(P2)+f(P3)+⋯, где T– этотрансцендентальная апперцепция, P1, P2 и т. д. – ряд последовательных перцепций, f – функция апперцепции. В обыденной ситуации интенция субъекта фиксирует своё внимание на некоторой точке A реального, за нею следует первичная перцепция, что можно обозначить как P1(A). Первичная апперцепция f(P1(A)), которая соотносится с членом ряда Тейлора f(A), является следствием самой сильной первичной перцепции. Следующим шагом воображаемое и вторичные перцепции, порождая вторичные апперцепции, достраивают реальное до некоторого объективного, что обозначено следующим членом f(P2), соотносящегося со вторым членом ряда Тейлора df(A)/dx dx, затем третичные апперцепции f(P3) – (d^2 f(A))/〖dx〗^2 〖dx〗^2+⋯ и т. д.. Процесс трансцендентальной апперцепции можно представить образно на примере внезапного обнаружения слона в джунглях: тогда f(A) будет обозначать абстрактный тёмный объект-куб (форма слона), следующие члены ряда придадут контрастность кубу, определят его как живое, добавят деталей в виде ушей, хобота, цветовой палитры, жевания травы и т. д. (При условии, что представления об ушах, хоботе, цветовой палитре и жевании травы уже присутствуют априорно или апостериорно). После чего абстрактный объект-куб превращается в определённого слона – каждый следующий, пусть и уже малый член такого ряда апперцепций добавляет уникальность объекту интенции. И чем больше ряд T=f(P1)+f(P2)+f(P3)+⋯, тем большую семантическую область удастся означить, тем существеннее будет ∆x – область семантического определения.
Уточним, что математический термин «гладкая функция» в нашем контексте означает, что конституирование символической формы образа объекта посредством ряда перцептивных уточнений объекта происходит последовательно, одновременно расширяя область семантического представления об объекте. Например, если после обнаружения змеи, в результате очередного итерационного перцептивного шага определится, что у змеи есть лапы, то образ змеи сингулярно переместится в иную часть семантики, где змея окажется ящерицей. В данном примере функция трансцендентальной апперцепции гладкой не будет.
Поскольку понятие смысл близко к понятию информация, то неудивительно, что такое представление об эволюции символических форм коррелирует с предложенным Германом Хакеном алгоритмом распознавания образа [16, с. 211]. Если алгоритм традиционного распознавания строится на анализе образа, на его разделении на составляющие, распознавании каждой части отдельно и последующей обратной сборке в искомый образ, то в его варианте «на первом этапе образ воспринимается на глобальном уровне, на котором возможны переходы из начального состояния в несколько аттракторов. Затем включается сенсорная система, позволяющая учесть дополнительные особенности изображения и тем самым выбрать более тонко детализированное множество аттракторов» [16, с. 47]. Понимание притягивающего аттрактора Хакеном и нами идентично – это некий образ (идея), к которому тянется сущность. И образ, как в предыдущем примере, может пойти по пути змеи или ящерицы, поскольку они похожи, и только их детализация определит, какой аттрактор – змеи или ящерицы – наблюдается в действительности. Последующие (уже более гладкие) уточнения определят вид конкретной змеи или ящерицы (например, это гадюка или медянка).
В последнем примере конституирующий ряд апперцепций T=f(P1)+f(P2)+f(P3)+⋯ означает определение последующих, более тонких производных, которые, как уже писалось выше, характеризуют изменение предыдущих (подобно тому как протуберанцы изменяют форму поверхности Солнца). Таким образом, последовательность апперцепций в точке A имеет когнитивный смысл – расширение семантической области мировосприятия позволяет, в свою очередь, расширить перцептивные возможности субъекта. Такое представление согласуется с понятиями антропологической эволюции, интуиции и её дальнодействия, что будет более подробно описано ниже. Одним из главных эволюционных шагов в антропологическом развитии было появление символических форм, выражающихся в математических формулах. Подстановка в эти формулы соответствующих перцептивных данных, качество которых растёт за счёт использования датчиков, более чувствительных, чем датчики, которыми обеспечила субъекта природа, позволяет расширить иерархию трансцендентальной апперцепции, увеличить количество членов ряда Тейлора, охватив не только геометрию объекта, но и его динамические аспекты (парадокс того, что прогноз погоды при всех современных аппаратных средствах действителен максимум на неделю, тогда как опытные древние люди могли прогнозировать погоду до полугода, разрешается конфликтом интеллекта и интуиции).
Иерархия перцепций связана с иерархиями нарратива (причинно-следственной иерархии), в котором располагается исследуемый объект, и внутренней иерархией самого объекта. Например, в образе слона контрастность пигментации кожи и наличие ушей и хобота относится к иерархии перцепций самого объекта, но процесс жевания травы через акт воображения связывает нас с местом, где он мог её сорвать и, соответственно, с влиянием внешней среды на объект. Можно обратить внимание, что, несмотря на общую гладкость апперцепции (не считая примеров, подобных переходам змея-ящерица), она имеет квантовый характер конституирования мышления – функция трансцендентальной апперцепции от добавления очередного перцептивного члена ряда меняется всегда скачком. Очередная перцепция пусть и незначительна по своей информативности, но тем не менее добавляет вполне конкретную величину информации, которая может запустить необратимый процесс, по аналогии с мостом, превышение отклонения которого приводит к его разрушению.
Ещё Гегель заметил, что разные члены ряда Тейлора, которые он назвал моментами, имеют качественно разную природу, действительно dx– это длина, 〖dx〗^2=ds – это площадь, 〖dx〗^3=dv – это объём. Философ в [4, с. 257] уделил большое внимание онтологии дифференциального исчисления и проблеме отбрасывания более высоких производных. Гегель писал о том, что различные объяснения подобного пренебрежения следующими членами ряда не вызывают доверия, а также о том, что каждый следующий член несёт в себе онтологический смысл последующего увеличения размерности, и, соответственно, члены ряда несопоставимы. «В механике членам ряда, в котором разлагается функция какого-нибудь движения, придаётся определённое значение, так что первый член или первая функция соотносится с моментом скорости, вторая с силой ускорения, а третья с сопротивлением сил. Поэтому члены ряда должны рассматриваться здесь не только как части некоторой суммы, но как качественные моменты некоторого понятия как целого. Благодаря этому отбрасывание остальных членов, принадлежащих к дурно бесконечному ряду, имеет смысл, совершенно отличный от отбрасывания их на основании их относительной малости» [4, с.282]. Иными словами, отбрасываемые, якобы малые члены ряда могут на равных фундировать значение функции. Такие моменты Пригожин и Хакен назвали точками бифуркации.
Нужно обратить внимание на другой аспект, хорошо видимый из диаграммы аппроксимации реальности, приведённой ниже. Если Гегель указал на разную природу множителейdx,〖dx〗^2,〖dx〗^3 и невозможность их сопоставления, то необходимо указать на то, что множители df(A)/dx, (d^2 f(A))/〖dx〗^2 , (d^3 f(A))/〖dx〗^3 имеют разный масштаб воздействия и отвечают за иерархию дальнодействия.Иными словами, очередной член ряда Тейлора приближает объективное к реальному на большеммасштабе (в случаеслона таким масштабом будет биологическая иерархия: семейство, род, вид, и иерархия нарратива: областьохватываемых джунглей). Диаграмма аппроксимация реальности, демонстрирует изменение дальнодействия вместе с учётом всё большего членов ряда, некий «взгляд за горизонт»:
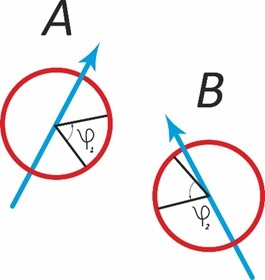
Для возможности интерференции сущностей A и B, при которой происходит нелинейное сложение, необходимо их фазовое согласование , в противном случае их взаимодействие сведётся к статистическому варианту 2+2=4. В случае статистического описания множества сущностей (газ, заключённый в сосуд, множество людей, идущих по улице) понятие фазы, усредняясь, теряется. Конечно, не нужно представлять человека подобным волчку, вращающемуся вокруг оси, как и спин электрона не нужно представлять просто в виде вращающейся сущности. Ключевым здесь является то, что любая сущность определяется двумя параметрами – амплитудой A и фазой φ, точнее говоря, их наборами A(i)∑_i〖w(i)〗 .Таким образом, волновая природа – это некоторая инвариантность, описывающаяся двумя параметрами – амплитудой A и фазой φ, где φ можно определить традиционно φ=wt-kx , где w–частота осцилляций, k–волновой вектор. Этими же двумя параметрами – амплитудой A и фазой φ– определяются комплексные числа. Чтобы понять резонансные эффекты, необходимо несколько углубиться в свойства комплексного числа.
Краткая история чисел
Традиционно считается, что в основе описания всех феноменов лежат действительные числа, которые описывают действительность. Но цельность такого описания, как некоторый числовой гештальт, как некоторая замкнутость описания феноменального, находится не над полем действительных чисел, а над полем комплексных (находиться над полем означает использовать их в качестве аргумента). Если образом действительных чисел является прямая, которая обладает когнитивной активностью (её можно продолжать бесконечно), то образом комплексных чисел является круг, который замкнут и становится инертен. Представление о числовом гештальте, как некоторой законченности, можно дать метафорически, на примере молекул глюкозы, чаще всего использующихся клетками по причине их замкнутости и неагрессивности, в отличие, например, от длинных, линейных молекул типа фруктозы, ведущих себя агрессивно и разрушающих клетки. Подобно этому, только замкнутая теория может быть идеальной и соответствующей некоторой устойчивой картине, но таковая (как будет показано ниже) может быть основана только на комплексных числах.
Почти очевидно, что исторически первыми появились натуральные числа от 1 до 3, идея которых долгое время вырабатывала свою когнитивность и осциллировала вокруг некоторого устойчивого значения: «первые свидетельства того, что числа больше двух когда-то объединяли в понятие «много», мы находим в истории пятитысячелетней давности» [7, с. 105]. Каждой цифре пифагорейцами был придан определённый сакральный смысл. Кроме того, исторически осциллировало само визуальное написание цифр (добавлялся и исчезал их орнамент), приняв окончательный вид только в девятнадцатом веке.
Первоначально, до открытия нуля, после девяти могли идти следующие цифры – где-то считали не десятками, а, например, двадцатками. «Среди прочих оснований систем счисления, который применяли некоторые народы по всему миру, самым популярным оказалось 20 (двадцатиричная система счисления)» [7, с. 37]. Очевидно, что это было связано с тем. что у человека двадцать пальцев. Первый существенный синтез в числовых представлениях произошёл вместе с открытием нуля, который является математическим воплощением философского понятия ничто (которое не стоит относить к числам, поскольку его природа индивидуальна). Ноль открывали многократно, и многократно теряли его, по той причине, что он не несёт оттенка имманентного, который присущ обычным числам, необходимым нам для обыденного счёта. Но помимо числа ноль было придумано трансцендентальное число бесконечности ∞. Следующая диаграмма показывает общность их природы и некоторую симметричность в представлении.
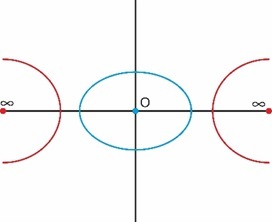
То, что ноль и ∞ можно приравнять друг другу, хорошо видно из теории квадратичных форм, которые в общем виде описываются формулой: 〖ax〗^2+by^2+dx+cy+k=0(и которые определяют всю современную физику: скалярное произведение, гамильтонову механику и т.д.).Известно, что есть несколько их основных типов: гипербола, эллипс, парабола и прямые. На диаграмме выше изображены эллипс и гипербола. И та, и другая кривая очень часто встречаются в реальности, в отличие от остальных вырожденных (уникальных) случаев. Эллипс и гипербола широко представлены в волновой механике, например, в оптике, в космологии и т.д. Все космические тела движутся либо по замкнутым эллиптическим орбитам (например, Земля вращается вокруг Солнца по эллипсу, где Солнце находится в одном из его фокусов), либо по разомкнутым орбитам гипербол. Но не сложно, рассматривая диаграмму, обнаружить, что разомкнутые орбиты гипербол на самом деле являются орбитами эллипсов, замкнутых вокруг точки ∞, иными словами, ни одно тело, покинувшее солнечную систему, не перестаёт осциллировать вокруг Солнца, только теперь центр Солнца перемещается в точку ∞. Можно сказать, что произвольная траектория есть комбинация эллипсов и гипербол, тело движется вокруг набора центров масс (вокруг земли, вокруг солнца и т. д.). Таким образом, точки 0 и ∞ являются дополнительными друг другу, и по одной точке можно восстановить другую. Данное геометрическое отступление от истории числа было необходимо, чтобы отметить тождественную природу понятий нуля и бесконечности.
Одновременно с открытием нуля был сделан следующий шаг – открытие числа 10. Можно обратить внимание на то, что, если обычное сложение выполняется аналитически: 1+0=1, то следующее сложение выполнено синтетически: 1+0=10, если первый подход можно назвать декартовым или дедуктивным, то второй способ – это скорее эзотерика.
Дальнейшая история числа – это постоянное пополнение возникающей нехватки. Математическое понятие полноты характеризует, что любые разрешённые действия над некоторым множеством объектов оставляют результат действия внутри этого множества. В связи с обратным понятием неполноты уместно вспомнить притчу про слепых мудрецов, ощупывающих слона, которые идентифицировали его по некоторым деталям, например, хоботу, сообщая, что слон как змея. Но при передвижении вдоль теласлона происходит расширение образа, пока он не замкнётся и не станет полным. В контексте чисел неполнота означает, что выполнение некоторой разрешённой операции внутри определённого множества (например, сложение внутри множества чисел от 1 до 9)выводит результат операции за пределы множества собразованием нового числа, например, 9+3=12, и этот результат не находится в изначальном множестве, в отличие, например, от случая 3+4=7. В результате такого последовательного расширения сформировалось понятие натуральных чисел, обозначаемое буквой N. Напротив, весь ряд натуральных чисел замкнут относительно такой операции – сложение любых двух чисел остаётся внутри такого ряда. Но если осуществить обратную операцию вычитания, то она выведет нас из первоначального множества, обнаружив его неполноту. Например, операция 3-7=-4образует число минус четыре, не определённое ранее, что заставляет пополнить ряд натуральных чисел до ряда целых чисел. Такое число, как -4,было непонятным в обыденной жизни, но позже появилось его феноменальное отображение в качестве денежного долга.
Нужно обратить внимание на важный аспект: обратная операция никогда не является зеркальной и всегда выводит из зоны первоначального определения множества к новым объектам, таким образом действие и обратное действие не всегда являются симметричной конструкцией. В теории групп, описывающей симметрии универсума, элементами которой являются некоторые действия (повороты, отображения, растяжения и т. д.),имеется важное понятие об обратном элементе, т.е. если имеется некоторое действие, то должно быть и обратное. Последовательное осуществление прямого и обратного действий приводит к первоначальному состоянию, такая комбинация действий называется identity. Но именно спонтанное нарушение симметрии, известное в квантовой механике, приводит к синтезу новых объектов, подобно обратному действию в математике, нарушающему её замкнутость и симметричность (можно сказать, что весь видимый мир образовался не благодаря симметрии, а вопреки ей, поскольку он сформирован её нарушениями).
Таким образом, вместе с операцией сложения была определена операция вычитания. Но таким же образом к операции умножения (которая также оставляет числа внутри первоначального множества натуральных чисел) добавилась обратная операция деления и, как следствие, вновь потребовалось пополнение понятия числа, и так появились рациональные числа или дроби, типа 3/5.
Следующим шагом было появление иррациональных чисел, которые впервые возникли при попытке рассчитать длину гипотенузы треугольника или диагонали квадрата. Согласно формуле Пифагораa^2+b^2=c^2, диагональ квадрата со стороной 1 равна√2=1.414... Подобное расширение (пополнение) множества рациональных чисел иррациональными вновь возникло вместе с введением операции, обратной возведению в степень и называемой извлечением корня.
В результате пополнения рациональных чисел иррациональными оказалось, что основная масса чисел на числовой оси как раз иррациональные, они пополняют числовую ось до состояния битком, когда туда добавить что-либо уже невозможно, и тогда появилось понятие действительного числа, обозначаемое R.
Нужно упомянуть гениального математика Георга Кантора (1845-1918), который много сделал для теории множеств, в том числе, ввёл понятие мощности множества. Понятно, что пересчитать даже натуральные числа невозможно, их число бесконечно. Кантор придумал способ сравнения бесконечностей– два множества имеют одинаковую мощность, если между ними можно установить изоморфное отношение. Две базовые бесконечности –это счётная бесконечность (совокупность натуральных чисел) и континуум (совокупность действительных чисел). К великому удивлению Кантора мощность рациональных чисел и натуральных оказалась равной (т.е. рациональные дроби можно пересчитать при помощи натуральных чисел). В отличие от этого, иррациональных чисел уже существенно больше – сосчитать их при помощи натуральных невозможно. Чтобы ощутить соотношение рациональных и иррациональных чисел, можно образно представить, что все рациональные числа –это звёзды, просвечивающие сквозь плотные облака иррациональных чисел.
Можно несколько иначе выразить онтологию рациональных и действительных чисел: если первые порождены операцией сложения, последовательное применение которой приводит к умножению, то вторые порождены умножением и, как следствие, возведением в степень, иными словами, если N– количество натуральных чисел, то число вещественных чисел 2^N. Для того, чтобы представить, как быстро увеличивается число 2^N сростом N, известный математик Михаил Громов привёл такой пример: если не ограничивать рост колонии бактерий, которые делятся в среднем каждые двадцать минут, то через семь дней размер колонии, стартовавшей с единственной бактерии, превысит размер видимой вселенной. Это же число 2^N характеризует собой суперпозицию всех натуральных чисел, иными словами, количество способов которыми возможно скомбинировать все натуральные числа. Возникает вопрос, сколькими способами можно скомбинировать все действительные числа и соответственно какова суперпозиция всех действительных чисел? По-видимому, можно предположить, что следующая мощность бесконечности2^(2^N ).
В истории известно много попыток пополнить множество действительных чисел, и многие из них были успешны, хотя пока и не прижились(не вошли в область априорного), например, теория гипердействительных чисел или теорияp-адических чисел. Можно сказать, что p-адические числа – это попытка представить числовую ось неоднородной, а иерархичной. Когда мы смотрим на неё, то в силу ограниченности силы нашего зрения видим её в виде единой прямой, хотя на самом деле она имеет внутреннюю структуру, и если посмотреть на числовую ось «через микроскоп», то можно обнаружить фрактальность числовой оси, где в основе фрактала лежат простые числа.
Комплексные числа, также как иррациональные, явились пополнением известного до них множества чисел, которое было вызвано операцией, обратной возведению в степень, т.е. взятием корня из отрицательного числа, что приводит нас к понятию мнимой единицы√(-5)=√5×√(-1)=i√5. Мнимая единица i=√(-1)оказалась последним объектом, необходимым для замыкания числовой алгебры –любые возможные действия над комплексными числами оставляют результат в поле комплексных чисел. Конечно, такое утверждение истинно при условии, что не появится новое алгебраическое действие в поле комплексных чисел помимо сложения, умножения и возведения в степень.
Одним из первых, обнаруживших конструкцию мнимой единицы, был Кардано (1501-1576), который так и оставил её в области экзотики. Когда Иоганн Карл Фридрих Гаусс (1777-1855) обнаружил комплексные числа, он побоялся публиковать результаты, опасаясь, что его поднимут на смех, и назвал √(-1) мнимой, (лживой) единицей. Именно Гаусс доказал полноту алгебры комплексных чисел (любые действия, известные в математике с комплексными числами, имеют результат в поле комплексных чисел). Комплексные числа, обозначаемые буквой Z, расширяют область определения чисел из одномерного пространства числовой оси до плоскости и представляются в виде a+bi, подобно двум координатам на плоскости, где i– мнимая единица. Действительное число a откладывается по оси x, тогда как действительное число b при мнимой единице откладывается по оси y, как изображено на диаграмме.
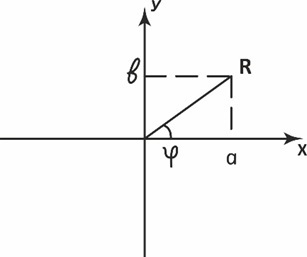
Таким образом, a+bi определяет диагональ треугольника со сторонами a и b. Но эту же диагональ можно выразить через её длину R и угол φ, тогда a=R×cosφ, b〖=R×sin〗φ, подставляя эти выражения в формулу a+bi= R×cosφ+i〖R×sin〗φ=R×(cosφ+isinφ)=R×e^iφ, здесь последнее преобразование –это известное тригонометрическое тождество. Видно, что комплексное число определяется радиус-вектором R и углом φ междуосью x и этим радиус-вектором R, иными словами, комплексное число выражается через его амплитуду R и фазу φ,что определяет фундаментальную пару для полного описания сущности, о чём говорилось выше, в отличие от традиционного, ограничивающегося только амплитудойR(энергетического описания сущности).
Представление о комплексных числах нашло множество реальных применений в волновой механике: при описании электромагнитных полей, в квантовой механике и в гораздо более прозаической науке электротехнике, где, как известно, помимо реального сопротивления резисторов имеется мнимое сопротивление катушек и конденсаторов, но это мнимое сопротивление оказывает вполне реальное влияние на многие электромагнитные процессы.
Уильям Гамильтон (1805-1865) создал теорию кватернионов (которые на тридцать лет раньше открыл Гаусс, назвав такие числа мутациями), обобщение комплексного числа, но уже в четырёхмерном пространстве. В таком пространстве мнимых единиц уже три: i,j,k, их алгебра строится на нескольких коммутационных соотношениях: i^2=j^2=k^2=i×j×k=-1, и между собой i×j=-j×i и т. д., вид кватерниона в общем виде следующий: q=a+bi+cj+dk. Кватернионы также замкнуты внутри своей алгебры, но всё-таки комплексные числа имеют более фундаментальную природу, поскольку кватернионы строятся, исходя из алгебры комплексных чисел, и могут быть представлены как q=z+wj, где z и w, в свою очередь, комплексные числа. Таким образом, двумерные комплексные числа расслаиваются в четырёхмерное пространство кватернионов. (Интересно, что все n-мерные пространства делятся на чётные, внутри которых существует замкнутая алгебра, подобная комплексным числам и нечётные, где это невозможно, чётные пространства n можно представить как n⁄2×z–произведение n⁄2 комплексных пространств). Можно продолжить удвоение размерности и построить замкнутую алгебру октав в восьмимерном пространстве чисел вида t=q1+lq2, где l ещё одна мнимая единица, а q1 и q2 –кватернионы. Несколько другим путём пошёл Роджер Пенроуз, создав теорию твисторов, соединив четырёхмерное пространство-время и комплекснозначность бытия. Таким образом, выстраивается числовой фрактал, в основе которого лежат комплексные числа. Несмотря на вторичность кватернионов, благодаря им был дан существенный толчок математике, приведший к концептам матриц и линейных операторов. Теория кватернионов в настоящее время вновь активно используется в квантовой теории поля.
Но помимо того, что кватернионы являются производными от комплексных чисел, они теряют такое важное качество как коммутативность умножения, а октавы ещё и ассоциативность. Поэтому мы можем попробовать ввести понятие когнитивности числа, которое определяет сумму возможностей, которыми обладает данное поле чисел. Здесь возможности – это область покрытия чисел, и операции, которые демонстрируют богатство алгебры: коммутативность, ассоциативность, дистрибутивность и т. д. Тогда несложно обнаружить следующую диаграмму, где буквы N, Z, Q и т.д. означают категории: натуральных, целых и т. д. чисел. Здесь видно, что комплексные числа C обладают максимумом когнитивности.
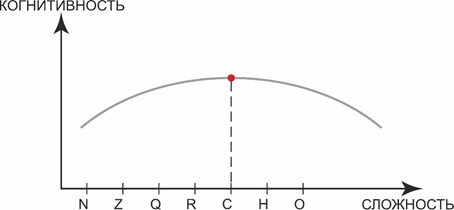
Конечно сложно сравнивать, например, натуральные числа и комплексные, также как отдельную берёзу и какой-нибудь лес – и то, и другое – уникальные объекты разного масштаба. Но нас в данном случае интересует возможность описания при помощи этого объекта (комплексных чисел) физических экспериментов.
Волновая физика
Центральным представлением в волновой механике является волновое уравнение д'Аламбера: □u=0, которое возникает во всех областях физики и других сопряжённых с ней наук (химия, биология, социология), и разрешается при помощи комплексных чисел, представляясь в виде суперпозиции двух свободных волн, в одномерном случае движущихся в плюс бесконечность x и минус бесконечность -x:〖 ae〗^(iwt+ikx)+be^(iwt-ikx), где w – частота волны, а k и –k – волновые вектора, задающие направление движения волны. Ограничение, называемое в физике граничными условиями, превращает свободные волны в определённый волновой цуг, сепарируя весь континуум частот, до определённого количества, подобно тому как экологическая ниша (понятие введённое в биологии, для определения существования некоторого вида и являющееся совокупностью внешних параметров: места обитания вида, температуры в месте обитания и т. д.) определяет вид животных, осциллирующих внутри ниши (закон о существовании единственного вида внутри одной экологической ниши обнаружен Гаузе [Гаузе]), аналог закона Паули в квантовой механике (так же, как внешние и внутренние условия налагают ограничения на социальные осцилляции, например, осцилляции семьи). Именно граничные условия определяют собственные волновые функции, подобно тому как длина струны определяет её звучание (прижимая струну пальцем к грифу, гитарист меняет экологическую нишу и меняет собственное значение волновой функции).
Рассмотрим подобное представление в случае уже упомянутого двущелевого эксперимента, когда на две щели падает световой пучок, и, проходя через них, на заднем экране образует интерференционные эффекты. Если частоты двух источников совпадают, тосуммарная интенсивность света от двух пучковна заднем экране: I=〖e^iwt (ae〗^ik1x+be^ik2x)e^(-iwt) 〖(ae〗^ik1x+be^ik2x)*=a^2+b^2+abe^(i(k1-k2)x)+abe^(i(k2-k1)x)=a^2+b^2+ab〖(e〗^(i(k1-k2)x)+e^(-i(k1-k2)x))= a^2+b^2+2ab cos〖(k1-k2)x〗,где a и b амплитуды света от разных отверстий. При равных a и b интенсивность осциллирует от 4a^2до нуля и мы наблюдаем удвоение когерентной интенсивности против статистической интенсивности, где было бы только 2a^2. В данном случае щели и экран определяют граничные условия, они являются тем пальцем, который прижимает струну к грифу.
Интерпретация волновой функции в квантовой механике, данная Максом Борном (1882-1970) гласит, что вероятность обнаружить частицу равна квадрату волновой функции P=φ×φ*, где * означает комплексное сопряжение,(a+ib)*=a-ib, уже использованное выше. Борн говорил, что сама волновая функция не имеет реального смысла, а является некоторой математической абстракцией. Как видно из определения комплексного сопряжения, оно означает отражение относительно оси x, но обратная волна, бегущая навстречу первоначальной, и есть та же самая волна, отражённая от некоторой границы, расположенной впереди. Таким образом, интерпретация Макса Борна просто постулирует, что наблюдаема только интерференция волн, но не сами волны. Интерференция как бы пригвождает волну, актуализируя её, делая её имманентной. Например, при игре на гитаре мы слышим звук интерференционного паттерна, образуемого прямой и обратной волной, бегущих по струне. В случае, если бы вероятность обнаружить частицу выражалась иначе, напримерP=φ×φ= 〖A^2 e〗^i2wt,т. е. без сопряжения, то как уже писалось выше, вследствие усреднения фазы стало бы равно 0, и сущности стали бы ненаблюдаемы. Таким образом, весь наблюдаемый мир – это результат интерференции, приводящий к его темпоральнойустойчивостиφ×φ*, когда прямая волна e^iwt и обратная волна e^(-iwt) совпадают по частоте и тогда φ×φ* не зависит от времениe^iwt e^(-iwt)=e^0=1. Таким образом определяется внутренняя устойчивость сущности.
Можно представить, как атомы, интерферируя друг с другом, образуют устойчивые состояния кристаллов. Здесь уместно вспомнить критику А.А. Власовым[2] традиционной науки, которая рассматривает кристалл как данность. Власов писал, что необходимо рассматривать кристаллы в их становлении, в связи с чем возникает вопрос: а можно ли создать когерентное состояние кристалла из десяти, ста, тысячи атомов?
Отражённая волновая функция определяется граничными условиями (волновая функция отражается от собственных границ и осциллирует внутри), которые, в свою очередь, определяет экспериментатор, поэтому наблюдаемая интерференция, определяющая сущность, фундируется экспериментатором. Так называемый коллапс волновой функции – это интерференция волновых функции объекта и прибора, которая как бы связывает волновую функцию объекта. Можно сопоставить физический эксперимент и речевой акт, и вспомнить представление Делёза, что любое предложение, помимо логики текста и предмета, о котором выражается мысль, всегда содержит внутри себя субъективную составляющую, иными словами, философию субъекта, изрекающего предложение[3]. Но речь –это такой же волновой процесс, актуализирующийся в виде предложений, устойчивых интерференционных паттернов звуков, причём сложностный волновой процесс, поскольку он имеет и волновую артикуляционную часть, и волновую смысловую часть. Таким образом, граничные условия, определяющие содержание (набор собственных функций)и физического эксперимента, и речевого акта во многом определяются индивидом.
Но из физики известно, что любая интерференция нескольких сущностей –от относительно простых(электронов в эксперименте Дэвиссона и Гермера, атомов в подобных экспериментах, световых лучей в опыте Юнга) до несопоставимо более сложных (индивидов в семье, социальных акторов внутри большего актора, например, цехов на предприятии), имеет ограниченную временную устойчивость, иными словами темпоральную длительность. В действительности разность фаз пусть медленно, но зависит от времени:φ1-φ2=const(t), поскольку частоты никогда не равны друг другу тождественно,w1-w2≠0(например, спектр излучения атома водорода имеет фрактальную структуру, поскольку излучение единичного атома всегда модулируется его окружением), таким образом, const является константой только некоторое время, подобный эффект в физике называется дисперсией. Если некоторое время темпоральностью сущности можно пренебречь, иными словами, такая зависимость незаметна, то через определённый промежуток времени наступает фазовое рассогласование и сущность теряет устойчивость. (Исключением являются запутанные объекты, где, по видимости, частоты совпадают абсолютно, и поэтому дисперсия равна нулю).Такая интерпретация эксплицирована в модели нелинейного осциллятора, где виден переход из гармонического этапа в хаотический. Таким образом, объективный мир представляет из себя «бурлящую интерференцию», где медленное «бурление»является модуляцией внутренних быстрых процессов и определяется темпоральным аспектом const(t), подобно тому как кипение жидкости и образование пузырей – является модуляцией быстрых внутренних термодинамических процессов. Дисперсия, или время дефазирования, характеризует темпоральность сущности, когда сущность перестаёт быть когерентной внутри себя, что, в свою очередь, определяет время её жизни, которое имеет определённое значение даже у таких стационарных структур, как периодический кристалл (алмаз), образовавшийся несколько миллионов лет назад. Дисперсия апериодического кристалла (ДНК), введённого Шредингером [16], время жизни которого в среднем составляет несколько лет, несопоставимо существеннее, хотя и имеет ту же природу. Очевидно, что имплицитно субъект подходит к вопросу о темпоральности, исходя из собственной длительности – декогеренция алмаза для него равна вечности и ненаблюдаема, в отличие от декогеренции ДНК, и здесь современный человек подобен древнему человеку, для которого число больше двух было «много». Индивиду понятнее время декогеренции, например, семьи, варьирующееся от месяцев до десятилетий, или время декогеренции нейтрона, распадающегося на электрон и протон за десятки минут. Темпоральный диапазон человеческой перцепции разнится от нескольких секунд (полёт пули) до нескольких столетий (ещё не затёртая память о нескольких поколениях). В последние два столетия перцепция человека существенно расширилась от фемтосекунд в ядерных процессах до миллиардов лет в геологии, благодаря аппаратным возможностям, но такая перцепция ещё не вошла в человеческое априорное.
Таким образом, сущность – это волновой, когерентный, интерференционный паттерн, который имеет некоторое время устойчивости, время когерентности. Необходимо отметить, что все наблюдаемые сущности, с одной стороны, внутри себя когерентны (атомы когерентны внутри молекулы), с другой стороны, две отдельные сущности сложно сделать когерентными между собой, по той причине, что более сложные сущности обладают большим набором собственных частот (экологическая ниша более сложной сущности имеет более сложную топологию). Если элементарные частицы (фермионы) имеют единственную внутреннюю (внешних, в составе которых осциллирует каждый фермион, например, вокруг Земли, бесконечно много) собственную частоту осцилляций, зависящую от их энергии по формуле w=E⁄ħ (это условно, поскольку большинство, а, возможно, и все они имеют составную природу), то уже молекулы имеют целый набор частот, определяемых внутренними степенями свободы ∑_i▒w 0 и внешними ∑_i▒w 1, т.е. такими осцилляциями, в которых молекула участвует как целое. Но для того, чтобы две сущности стали когерентными, необходимо фазовое согласование по всем частотам. И здесь мы приходим к фундаментальной лемме: две сущности, имеющие различный набор частот, притягиваются, но становятся целым, только если у них есть совпадение хотя бы части собственных частот. Иными словами, притягивает различие, но объединяет схожесть.Это можно выразить несколько иначе, если волновая функция сложной сущности φ1×φ2*, где φ1–волновая функция первой сущности, φ2–волновая функция второй сущности, то для образования устойчивого паттерна необходимо, чтобы сущности обладали как набором разных частот, благодаря чему осуществляется притяжение, так и набором равных частот, благодаря чему образуется устойчивый интерференционный паттерн, φ1=ae^(-iw0t) e^(-iw1t), φ2=be^(-iw0t) e^(-iw2t). Тогда притяжение осуществляется благодаря частотам w1 и w2, а объединение –благодаря общей частоте w0,φ1×φ2*=abe^(-i(w1-w2)t),–разное притягивает, одинаковое соединяет. Это несложно обнаружить в социальном – в противоположном поле на уровне интуиции всегда притягивает что-то отличное от собственного мировоззрения, но образовать устойчивую семью можно только на базе какой-то духовной общности.
Физика осторожно, шаг за шагом впускает комплексные числа в собственные теории. На наш взгляд, все объективные величины, входящие в физические законы, такие как, второй закон Ньютона F=m×a,должны иметь комплексный вид: F1+iF2=(m1+im2)×(a1+ia2). В работе [14] была предложена модель и интерпретация комплексной инертной массы в соответствии с представлением Маха о том, что в её формировании участвует вся Вселенная и, таким образом,m=m0+im1, где m0=∑▒w0 сумма всех внутренних осцилляций сущности, а m1=∑▒w1 - сумма всех внешних осцилляций (в составе планеты, солнечной системы, галактики и т. д.). Внутри такой формулировки можно обнаружить эволюционное усилие в направлении увеличения сложностности объекта в связи с ростом количества внутренних степеней свободы ∑▒w0.Увеличение количества ∑▒w0 увеличивает гибкость системы – она может встроиться в большее количество новых систем. Состав∑▒w0 обнаруживает преобразование Фурье, показывая частотную наполненность произвольного объекта. Как эволюционный скачок можно рассматривать переход от периодического кристалла к апериодическому кристаллу, когда произошло существенное увеличение числа внутренних свобод∑▒w0, и существенное усложнение материи. В математике есть понятие квазипериодичности, которое весьма возможно при большом количестве ∑w0 переходит в понятие апериодичности. Одновременно произошёл переход от неживой к живой субстанции.
Поскольку инертная масса есть способность сущности сопротивляться изменению, можно образно представить сущность как набор большого количества маленьких гироскопов, вращающихся с собственными частотами ∑▒w0, и сопротивляющихся пространственным изменения, что воспринимается как её инертность. Одновременно, собственные частоты определяются топологией внешних границ или краевыми условиями, и тогда вид сущности, определяется интерференцией прямой и отражённой волн S=(m0+im1)(m0+im1)*=(∑▒w0+i∑▒w1)(∑▒w0+i∑▒〖w1)*〗
Комплекснозначность означает присутствие макрочастот (внешних осцилляций, в которых сущность участвует как целое: вокруг Земли, Солнца и т. д.)наравне с микрочастотами (внутренних осцилляций) иимеет множественные экспериментальные подтверждения. Например, макрочастоты проявляются в микромире в тонких расщеплениях спектра, которые являются комбинацией множества разномасштабных осцилляций молекул (молекулы осциллируют в составе многих разномасштабных систем, расщепление спектра приводит к его фрактальной структуре [9]). В данном контексте необходимо упомянуть про работы С.Э. Шноля[15], который наблюдал присутствие этой бесконечной иерархии осцилляций в графиках различных гистограмм химических и ядерных процессов. Он рассматривает результаты химических процессов зависящими от сложной комбинации разномасштабных осцилляций.
Свидетельством того, что мир комплекснозначен, является множество различных фактов. Например, известное в математике качество аналитичности комплексной функции как условия Коши-Римана, которые являются аналогом уравнения гармонического осциллятора, т.е. локально комплексное пространство устроено подобно фазовому пространству осциллятора, иными словами, аналитичность (дифференцируемость) содержит уже в себе волновую онтологию.
Стандартная процедура современного физика – в случае неразрешимости уравнений – продолжение их в комплексную плоскость, решение уравнений в таком расширенном пространстве и последующая интерпретация результатов с возвращением на действительную ось. Самый простой путь – это узаконить комплекснозначную парадигму в физике и интерпретировать результаты соответственно ей.
В начале двадцатого века Давид Гилберт сформулировал свои, ставшие известными, 23 проблемы, в числе которых была 13-ая проблема, которую А. Н. Колмогоров переформулировал в возможность представления непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных. Приблизился к её решению В. И. Арнольд, доказав, что можно разложить функцию многих переменных в комбинацию конечного числа функции двух переменных и одной переменной. Наша идея состоит в том, что дальнейшее разложение невозможно, т. е. невозможно разложить функцию многих переменных в суперпозицию функций одной переменной, по причине того, что элементарным объектом такого разложения является функция комплексного переменного. В некотором смысле подобное разложение является разложением произвольной функции в ряд Фурье xe^iay. Это является ещё одной причиной комплексификации математики: «математики хорошо знают, что переход к комплексным числам обычно не усложняет, а упрощает задачу» [1, с. 77].
В книге «Красота фракталов" [12 ]авторы показывают фрактальность фазовых переходов и одновременно их комплекснозначность. «Фрактальность фазовых границ вполне может оказаться типичной. И тогда это будет призывом к исследованию физического смысла этого математического феномена» [12, с. 116].Но фазовый переход или точка бифуркации – это сингулярная точка синтеза в модели нелинейного осциллятора. Она порождает фрактальную онтологию, скачкообразно отделяя друг от друга два масштаба, и она же, согласно второму закону Гегеля, соответствует переходу количества в качество, т. е. фазовому переходу, когда появляется параметр порядка (введённый Ландау и описывающий по большому счёту некоторые масштабные осцилляции) более масштабный и отсутствующий до синтеза. В этой точке, с одной стороны, уже потеряна предыдущая когерентность (поскольку синтезу предшествовал этап хаоса), и, соответственно, сущность рассыпана на составляющие её элементы (наблюдается фазовое рассогласование), с другой стороны, приобретается новая фазовая когерентность и происходит мгновенное конституирование новой сущности. Таким образом, сам переход происходит в отсутствии когерентности, т. е. в множественном, статистическом виде.
В упомянутой книге [12]на примере фазового перехода между магнитным и немагнитным состояниями вещества рассмотрен вопрос комплекснозначности температуры и выход её на действительную ось при бесконечном количестве атомов, обозначаемый точкой Кюри. Магнитное состояние характеризуется наличием дальних связей и высоким уровнем когерентности, когда отдельные атомы пытаются выстроиться параллельно друг другу, тогда как немагнитное состояние описывается только ближними связями, когда атомы ведут себя практически независимо. Можно сопоставить описание дальнодействия с разложением намагниченности в ряд Тейлора (где каждый последующий член ряда имеет смысл увеличения масштаба рассмотрения когерентности), и тогда мы окажемся в дискурсе о значимости отдельных членов этого ряда. Напомним, что согласно Пригожину, в точке синтеза весь ряд Тейлора становится значимым. «Чем выше температура, тем меньше типичные расстояния и времена когерентности, а при очень больших температурах элементарные магниты могут изменять своё положение совершенно независимо друг от друга. Другие фазовые переходы также могут быть описаны как образование или разрушение дальнего порядка, при этом связь между температурой и пространственно-временными масштабами когерентности аналогична описанной выше» [12, с. 112]. Но при переходе в комплексную плоскость ряд Тейлора автоматически становится рядом Фурье, который описывает разложение функции по собственным частотам сущности, иными словами, по разным масштабам параметра порядка.
Было обнаружено, что на разных масштабах когерентность, и, соответственно, структурность имеет разный вид. Согласно Х.-О. Пайнтгена и П.Х. Рихтера, Л. П. Каданов предложил иерархию температур, соответствующих уровню масштабной упорядоченности (иными словами разной частотной насыщенности на разных масштабах). Температура перестала быть чем-то единым на всех уровнях. При температурах ниже, чем температура Кюри, по мере увеличения (огрубления) масштаба температура падает, приближаясь к абсолютному нулю на макромасштабе (если на наноуровне заметны флуктуации, то в сантиметровом диапазоне вид такой же как в районе нулевой температуры)и, наоборот, при температурах выше точки Кюри, по мере огрубления, температура растёт, устремляясь к бесконечности. В точке Кюри все масштабы подобны, все члены ряда Тейлора эквивалентны. Кроме того мы выдвигаем гипотезу, что броуновское движение — это не хаотическое прямолинейное движение, как это представляют в современной физической парадигме, когда происходит усреднение и ищется среднеквадратичное отклонение Δx=√t, а квазипериодические осцилляции частиц и их взаимодействия.
В контексте комплекснозначной парадигмы важнее другой аспект: физики Янг и Ли для решения задач, связанных с фазовыми переходами, решили выйти из области действительных чисел в поле комплексных. Они предложили рассмотреть многочлен c0+c1×x+c2×x^2+c3×x^3+c4×x^4+⋯+ cN×x^N=0, здесь N имеет значение количества атомов в рассматриваемом образце магнита, а x имеет смысл температуры. При положительных c такой многочлен не имеет корней в действительной области, но если выйти в комплексную плоскость, то многочлен приобретает N значений x, где он обращается в ноль. При N, устремляющемся к бесконечности, нули выстраиваются вдоль прямой перпендикулярной действительной оси и стремятся к ней обозначая таким образом точку Кюри, которая, очевидно, имеет реальный смысл. Позже выяснилось, что нули расположены вдоль достаточно сложной кривой, имеющей, в свою очередь, фрактальную структуру, в точности воспроизводящую множества Жулиа, образующиеся в алгоритме Мандельброта [12].
По нашему мнению, авторы совершенно зря боятся комплекснозначности температуры, благодаря которой можно определить точки Кюри для небольшого числа атомов, например, десяти или тысячи, выстраивая теорию микрокристаллов.
От физики к философии
В своё время Стивен Хокинг заявил, что когда-нибудь будет описана волновая функция всей вселенной, обозначив таким образом волновую онтологию универсума. Несложно догадаться, что эта функция описывает эволюцию Бога (хотя очевидно, что на Его уровне должна наблюдаться абсолютная темпоральная инвариантность), внутри которой будет запись о любом объекте. Но между волновой функцией атома и волновой функцией вселенной есть ещё очень длинная иерархия уровней, включая уровни человека, уровни социальных сущностей – акторов (социальных единиц), звёзды, галактики и т. д. Тогда волновая функция человека, подобно волновой функции атома, формируется как внутренними степенями свободы, так и экологической нишей, внутри которой он находится (хотелось бы употребить термин социальная ниша, но не будем, поскольку биологическое понятие экологической ниши значительно шире, оно учитывает, например, климатические эффекты, которые необходимо учитывать в социальных процессах), которая определяет граничные условия, внутри которых, в свою очередь, конституируются собственные значения индивида (устойчивые состояния). Как атом является экологической нишей для электрона, а кристаллическая ячейка является экологической нишей для атома, так и актор (социальная устойчивая система) является экологической нишей для индивида, и т.д., больший актор является экологической нишей меньшего, что показано на диаграмме, где красным обозначены собственные волновые функции различных сущностей на каждом иерархическом уровне. Максимальный масштаб ассоциируется с экологической нишей Вселенной, границы которой совпадают с её границами, модуляция которых приводит к осцилляциям сжатия-расширения. Следующий масштаб ассоциируется со скоплениями галактик и т. д.

Такое описание изоморфно описанию иерархии автоколебательных процессов, когда, с одной стороны, границы экологической ниши определяют набор собственных частот и, соответственно, вид единственной сущности (согласно принципу Паули или закону Гаузе), «обитающей» в ней (неживой или живой, соответственно), с другой стороны, эти границы сдвигаются, вследствие влияния экологических ниш ещё большего масштаба. Гаузе обнаружил, что внутри одной экологической ниши может существовать только один вид животных. Каждый уровень, с одной стороны, определяет собственную волновую функцию, с другой стороны, раскачивает внутренние ниши, влияя на более мелкий масштаб. Время t в каждом масштабе своё и отличается пропорционально некоторому параметру ε, τ=ε×t. Подобная иерархия наблюдается в турбулентности, когда крупный вихрь параметрически раскачивает более мелкие, распадаясь в них. «Пульсации первого порядка поглощают энергию осреднённого движения и передают её последовательно пульсациям более высоких порядков; энергия же самых мелких пульсаций рассеивается в тепловую благодаря вязкости» [6, с. 313]. В работе «Импеданс и параметрическое возбуждение осцилляторов» Б. Я. Зельдович [4], обнаружил, что параметрическое возбуждение происходит посредством влияния на импеданс, волновую инерциальную характеристику объекта (его сопротивляемость изменениям, расширяющую понятие массы), а не на частоту, его кинематическую характеристику. Напротив, если медленно изменять границы экологической ниши (которые определяют частотную характеристику объекта, как это указано выше), то некоторая структура, названная адиабатическим инвариантом (например, вид животных), не будет изменяться. Медленность здесь означает, что частота воздействия отсутствует в частотной характеристике объекта. Но как несложно заметить из диаграммы, время меньшего и большего масштаба всегда соотносятся как: τ=ε×t.
Именно через адиабатические инварианты произойдёт стык между квантовой механикой и макрофизикой, так же как образованное нами сближение между законами Паули и Гаузе. Необходимо пояснить, что параметрический резонанс и автоколебания – это разные описания одного и того же. Они различаются областями определений. В традиционном описании: первое – это изменение осцилляций системы, вызванное периодическим воздействием, второе – это колебания в диссипативной системе, вызванные непериодическим внешним воздействием. Обычно приводятся примеры автоколебаний: часы под воздействием груза, скрипичная струна под воздействием смычка. Но несложно заметить, что все эти механизмы непериодичны только локально – часы необходимо заводить, а смычок передёргивать в первоначальное состояние, более того, любое периодическое воздействие большего масштаба на меньший выглядит как прямолинейное воздействие, поскольку его кривизна в меньшем масштабе стремится к нулю пропорционально параметру ε.
Можно предположить, что центральной силой, запускающей автоколебательные процессы на всех уровнях, от вселенной до атома и глубже, является сила, расширяющая вселенную, которая нарушает закон сохранения энергии внутри границ вселенной. Такое расширение может выглядеть как прямолинейное радиальное движение, которое, подобно смычку, возбуждает автоколебания скоплений галактик, осцилляции которых (локально выглядящие как прямолинейное движение в рамках галактики) возбуждают автоколебания галактик, далее звёздные системы и т. д.
Многие процессы в природе верифицируют иерархичность автоколебательных процессов – турбулентность в гидродинамике, где внутри фрактального процесса вихри большего размера инициируют вихри меньшего размера, раскачивая их, ячейки Бинара, где вертикальный поток тепла (также, как в гидродинамике ламинарный поток при определённой скорости инициирует турбулентный) создает внутри сосуда сотовые структуры, которые можно считать собственными функциями циркуляции жидкости и которые определяются топологией сосуда (экологической нишей).
В работе [14] мы предположили, что символические формы (мемы, культурные коды, научные концепты и т.д.) эволюционируют согласно модели нелинейного осциллятора, поэтому символические формы также имеют волновые функции и собственные значения, которые приобретаются ими внутри некоторых смысловых ниш. Очевидно, что понятие смысловой ниши коррелируют с понятием экологической ниши, поскольку одно есть репрезентация другого. Посредством представления о волновой функции символических форм проясняется понятие множественности истины – поскольку форма осциллирует, то в зависимости от фазы она по-разному встраивается в общий контекст, образующийся как раз интерференцией внутри общего текста и, соответственно, меняет полярность, меняет истинность тех или иных суждений.
Субъект осциллирует не только видимым образом в четырёхмерном пространстве-времени, например, вместе с вращением Земли, но и во множестве более сложностных социальных систем, например, в рамках политической партии или в рамках семьи. Тогда субъективное время – это время наблюдения себя внутри какой-то одной системы. Сознание человека, находясь во временном континууме, достаточно быстро переключается из системы семьи к системе работы и, далее, к системе государства и обратно. Но, подобно тому как спин электрона может быть обнаружен только в одном направлении, человек может удерживать своё сознание, выражаясь квантовым языком, производить редукцию в рамках только одной системы. Он не может осознанно участвовать в нескольких процессах одновременно. Но бессознательно может. Подобно спину электрона, который находится, с некоторой вероятностью, одновременно в нескольких базовых состояниях, так и человек, находясь в бесконечномерном (гильбертовом) пространстве бессознательного, участвует в осцилляциях множества систем.
Попытка подобного представления экспликации волновой функции человека и квантовой природы сознания была сделана в работе Петренко и Супруна [13].Благодаря такой интерпретации в определённом смысле возможно соединить восточную иррациональную и западную рациональную философии. Можно заметить, что субъект участвует во множествеосциллирующих систем в некий момент времени∑_i▒w.При этом он, переключая сознание, входит в когерентное состояние с одной из них (семья, школа, спортивные секции, вращение Земли), но перцептивно он воспринимает их все. Они все формируют мнимую часть его волновой функции, из которой субъект конституирует всё кантовское многообразие в определённый момент времени, захватывая небольшие темпоральные участки ретенции и протенции. Можно предположить, что, входя в процессе медитации в так называемое измененное состояние, индивид переключается из временной координаты в частотное измерение и созерцает одну-единственную систему с присущей ей определённой частотой на всём протяжении, от бесконечного прошлого до бесконечного будущего. Иначе говоря, мозг в состоянии медитативного транса производит преобразование Фурье ∑_i▒w→∑_i▒tи наблюдает единственную систему, в рамках которой он осциллирует, частично захватывая частотные ретенцию и протенцию. Человек переходит из временного континуума в частотный.
Следствием представления о запутанности волновых функций(их неразличимости) индивидовдолжна явиться телепатия. Ещё в пятидесятые годы К. Юнгом была выполнена работа [17], где Юнг, работая с Паули, описывал множество случаев, которые невозможно объяснить рационально. Но совершенно несложно представить, что если волновые функции двух субъектов запутаны, то символические формы появляются у обоих персон одновременно (социальная система может быть разнесена в пространстве, но тем не менее оставаться запутанной, связанной). Сложность заключается в том, что, в отличие от двух электронов, запутать двух индивидов сложнее, и они будут находиться в каком-то промежуточном состоянии. Запутанные частицы чаще всего вместе рождаются, так же как близнецы остаются в запутанном состоянии на всю жизнь. Возможно, запутывание происходит под высоким давлением внешних обстоятельств, таких, как любовь или война. Имеются многочисленные свидетельства психотерапевтов о таких явлениях у пациентов.
В рамках вышесказанного, продолжая идеи Шредингера [16]и Иваницкого[5], можно попробовать дать определение жизни. Иваницкий писал, что на протяжении жизни сердечные осцилляции имеют хаотическую составляющую, в результате чего траектория таких осцилляций имеет характер странного аттрактора, напротив, перед смертью хаотическая составляющая исчезает, и сердце начинает идеально осциллировать. Жизнь человека – это суперпозиция множества осциллирующих паттернов, начиная от вегетативных процессов, «семейных» и «служебных» осцилляций(одного темпорального масштаба с ними осцилляции вокруг Земли, поскольку они равны дневному циклу) и, наконец, государственных процессов(одного масштаба с ними осцилляции вокруг Солнца, годовой цикл) и, возможно, галактические процессы– это суперпозиция множества осцилляций, где их число превышает некоторое критическое значение (N<Nкритобъектовнеживой природы, N>Nкриту объектов живой природы). В свою очередь смерть – это редукция волновой функции в одно из базисных состояний, когда интерференция становится стационарной.
Литература
- Арнольд В.И. Теория катастроф. ЛЕНАНД, Москва. (2016).
- Власов А.А. Теория многих частиц. Книжный дом ЛИБРОКОМ, Москва. (2016).
- Делёз Ж. Логика смысла. Академический проект, Москва. (2015).
- Зельдович Б.Я. Импеданс и параметрическое возбуждение осцилляторов. Успехи физических наук, Т.178. №5. 489–510(2008).
- Иваницкий Г.Р. ⅩⅩⅠ век: что такое жизнь с точки зрения физики. Успехи физических наук,Т.180 №4. 339-369 (2010).
- Колмогоров А. Н. Избранные труды. Т. 1: Математика и механика. Наука, Москва. (2005).
- Ливио М.φ – число Бога. Золотое сечение – формула мироздания. АСТ, Москва. (2018).
- Мамардашвили М.К. Необходимость себя. Издательство «Лабиринт», Москва.(1996).
- Мандельброт Б. Фрактальная геометрия природы. Институт компьютерных исследований, Москва. (2002).
- Наварро Ф. Наука. Величайшие теории: выпуск 3: Гейзенберг. Принцип неопределённости. Существует ли мир, если на него никто не смотрит? https://www.rulit.me/books/nauka-velichajshie-teorii-vypusk-3-gejzenberg-princip-neopredelennosti-sushchestvuet-li-mir-esli-na--read-403201-15.html
- Рикёр П., Гадамер Х.-Г. Феноменология поэзии. Группа Компаний РИПОЛ классик / Панглосс, Москва.(2019).
- Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. – Мир, Москва. (1993).
- Петренко В.Ф. Супрун А.П. Методологические пересечения психосемантики сознания и квантовой физики. КРАСАНД,Москва.(2018).
- Стригин М.Б. Аналитический и синтетический этапы эволюции произвольных систем: онтологические особенности и характеристики. Современный учёный, № 8. 31–39(2018).
- Шноль С. Э. Космофизическая природа идеи формы гистограмм, построенных по результатам измерений процессов разной природы. Метафизика. Век ⅩⅩⅠ. Альманах. выпуск 2: сборник статей/ под ред. Ю.С. Владимирова. БИНОМ. Лаборатория знаний, Москва. С. 284–320(2007).
- Шредингер Э. Что такое жизнь с точки зрения физики?РИМИС, Москва.(2015).
- Юнг К.Г. Синхронистичность: акаузальный объединяющий принцип. Рефл-бук, Москва.Ваклер, Киев.(1997).
Reference
- Arnold V.I. Theory of catastrophes. LENAND, Moscow. (2016).
- Vlasov A.A. Theory of many particles. LIpOCOM Book House, Moscow. (2016).
- Deleuze J. The logic of meaning.Academic Project, Moscow. (2015).
- Zeldovich B.Ya. Impedance and parametric excitation of oscillators. Successes of Physical Sciences, Vol.178. №5. 489-510(2008).
- Ivanitsky G.R. век century: what is life from the point of view of physics. Successes of Physical Sciences, Vol.180 №4. 339-369 (2010).
- Kolmogorov A. N. Selected works. Vol. 1: Mathematics and Mechanics.Science, Moscow. (2005).
- Livio M.φ is the number of God. The golden ratio is the formula of the universe.AST, Moscow. (2018).
- Mamardashvili M.K. The necessity of self.Labyrinth Publishing House, Moscow.(1996).
- Mandelpot B. Fractal geometry of nature.Institute of Computer Research, Moscow. (2002).
- Navarro F. Science. The Greatest theories: Issue 3: Heisenberg. The uncertainty principle. Does the world exist if no one is looking at it? https://www.rulit.me/books/nauka-velichajshie-teorii-vypusk-3-gejzenberg-princip-neopredelennosti-sushchestvuet-li-mir-esli-na--read-403201-15.html
- Riker P., Gadamer H.-G. Phenomenology of poetry.Group Of Companies RIPOL classic / Pangloss, Moscow.(2019).
- Paytgen H.-O., Richter P.H. The beauty of fractals. Images of complex dynamic systems. - Mir, Moscow. (1993).
- Petrenko V.F. Suprun A.P. Methodological intersections of psychosemantics of consciousness and quantum physics.KRASAND, Moscow.(2018).
- Strigin M.B. Analytical and synthetic stages of the evolution of arbitrary systems: ontological features and characteristics. Modern Scientist, No. 8. 31-39(2018).
- Shnol S. E. The cosmophysical nature of the idea of the form of histograms constructed from the results of measurements of processes of different nature. Metaphysics. Century ⅩⅩⅠ. Almanac. Issue 2: collection of articles/ edited by Yu.S. Vladimirova.BINOMIAL. Laboratory of Knowledge, Moscow.pp. 284-320(2007).
- Schrodinger E. What is life from the point of view of physics?RIMIS, Moscow.(2015).
- Jung K.G. Synchronicity: the acausal unifying principle.Refl-book, Moscow.Vakler, Kiev.(1997).

